问题描述:
Use the following method printPrimes() for questions a–d.
/**
* Finds and prints n prime integers
* Jeff Offutt, Spring 2003
*/
private static void printPrimes(int n) {
int curPrime; //Value currently considered for primeness
int numPrimes; // Number of primes found so far;
boolean isPrime; //Is curPrime prime?
int[] primes = new int[MAXPRIMES];// The list of primes.
// Initialize 2 into the list of primes.
primes[0] = 2;
numPrimes = 1;
curPrime = 2;
while(numPrimes < n) {
curPrime++; // next number to consider...
isPrime = true;
for(int i = 0; i <= numPrimes; i++ ) {
//for each previous prime.
if(isDvisible(primes[i],curPrime)) {
//Found a divisor, curPrime is not prime.
isPrime = false;
break;
}
}
if(isPrime) {
// save it!
primes[numPrimes] = curPrime;
numPrimes++;
}
}// End while
// print all the primes out
for(int i = 0; i < numPrimes; i++) {
System.out.println("Prime: " + primes[i] );
}
}// End printPrimes.
(a) Draw the control flow graph for the printPrime() method.
ans:
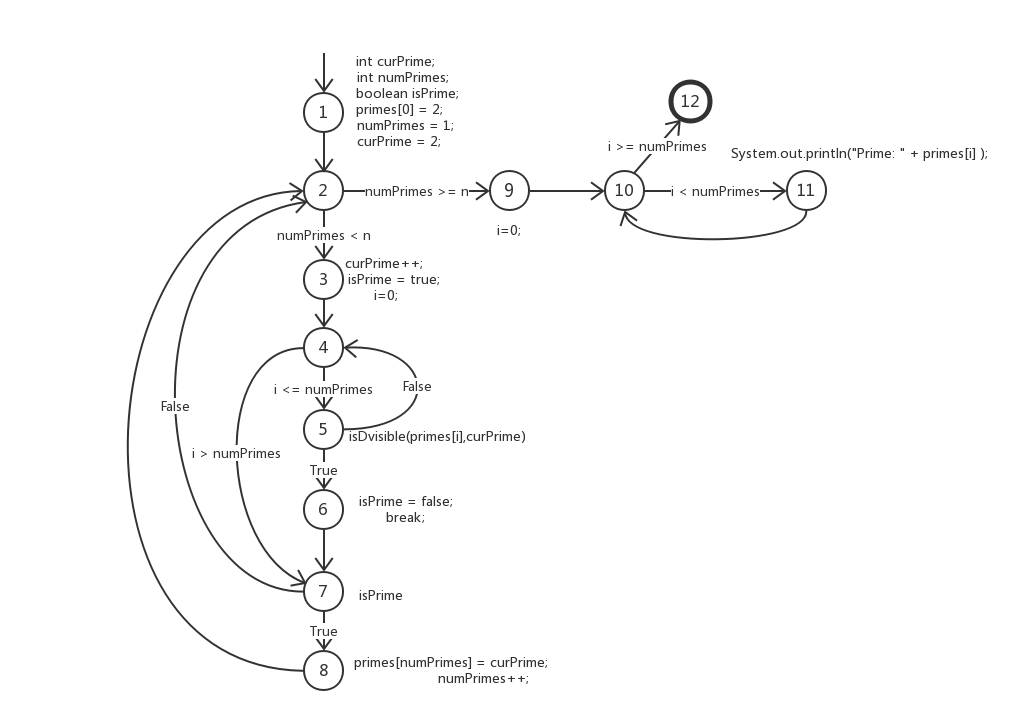
(b) Consider test cases ti = (n = 3) and t2 = ( n = 5). Although these tour the same prime paths in printPrime(), they don't necessarily find
the same faults. Design a simple fault that t2 would be more likely to discover than t1 would.
ans:
the condition of while statement: numPrimes < n -> numPrimes <= n-1
the condition of the for statement in while: i <= numPrimes -> i < numPrimes
(c) For printPrime(), find a test case such that the corresponding test path visits the edge that connects the beginning of the while statement
to the for statement without going through the body of the while loop.
ans: n = 1 or n = 0
(d) Enumerate the test requirements for node coverage, edge coverage,and prime path coverage for the path for printPrimes().
ans:
node coverage:
nodes: [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12]
test case: [1,2,3,4,5,6,7,8,2,9,10,11,10,12]
edge coverage:
edges: [1,2], [2,3], [2,9], [3,4], [4,5], [4,7], [5,6], [5,4], [6,7], [7,2], [7,8], [8,2], [9,10], [10,11], [10,12], [11,10]
test case: [1,2,3,4,5,4,5,6,7,8,2,9,10,11,10,12], [1,2,3,4,7,2,9,10,12]
prime path coverage:
prime path: [1,2,3,4,5,6,7,8], [1,2,3,4,7,8], [1,2,9,10,11], [1,2,9,10,12]
[2,3,4,5,6,7,8,2], [2,3,4,5,6,7,2], [2,3,4,7,8,2], [2,3,4,7,2]
[3,4,5,6,7,8,2,9,10,11], [3,4,5,6,7,2,9,10,11], [3,4,5,6,7,8,2,9,10,12], [3,4,5,6,7,2,9,10,12], [3,4,7,2,9,10,11], [3,4,7,2,9,10,12], [3,4,7,8,2,9,10,11], [3,4,7,8,2,9,10,12]
[4,5,4]
[5,4,5], [5,4,7,2,9,10,11], [5,4,7,2,9,10,12], [5,4,7,8,2,9,10,12], [5,4,7,8,2,9,10,11]
[7,2,3,4,5,6,7], [7,2,3,4,7]
[8,2,3,4,5,6,7,8], [8,2,3,4,7,8]
[10,11,10]
[11,10,11], [11,10,12]
test case: [1,2,9,10,12], [1,2,9,10,11,10,11,10,12]
[1,2,3,4,5,4,7,2,9,10,12], [1,2,3,4,5,4,7,2,9,10,11]
[1,2,3,4,5,4,7,8,2,9,10,12], [1,2,3,4,5,4,7,8,2,9,10,11]
[1,2,3,4,5,6,7,2,9,10,12], [1,2,3,4,5,6,7,2,9,10,11]
[1,2,3,4,5,6,7,8,2,9,10,12], [1,2,3,4,5,6,7,8,2,9,10,11]
[1,2,3,4,5,4,5,6,7,2,9,10,12], [1,2,3,4,5,4,5,6,7,2,9,10,11]
[1,2,3,4,7,2,9,10,12], [1,2,3,4,7,2,9,10,11]
[1,2,3,4,7,8,2,9,10,12], [1,2,3,4,7,8,2,9,10,11]