题目描述
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中,牌的大小关系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
具体规则如下:
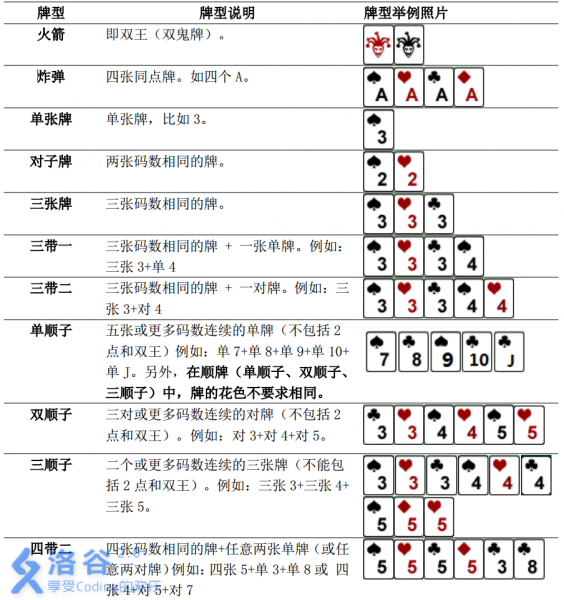
输入输出格式
输入格式:
第一行包含用空格隔开的2个正整数Tn,表示手牌的组数以及每组手牌的张数。
接下来T组数据,每组数据n行,每行一个非负整数对aibi表示一张牌,其中ai示牌的数码,bi表示牌的花色,中间用空格隔开。特别的,我们用1来表示数码A,11表示数码J,12表示数码Q,13表示数码K;黑桃、红心、梅花、方片分别用1-4来表示;小王的表示方法为01,大王的表示方法为02。
输出格式:
共T行,每行一个整数,表示打光第i手牌的最少次数。
输入输出样例
输入样例#1:
1 8 7 4 8 4 9 1 10 4 11 1 5 1 1 4 1 1
输出样例#1:
3
输入样例#2:
1 17 12 3 4 3 2 3 5 4 10 2 3 3 12 2 0 1 1 3 10 1 6 2 12 1 11 3 5 2 12 4 2 2 7 2
输出样例#2:
6
说明
样例1说明
共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
对于不同的测试点, 我们约定手牌组数T与张数n的规模如下:
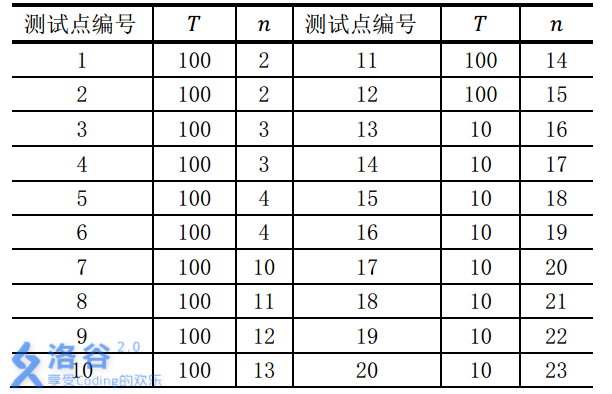
数据保证:所有的手牌都是随机生成的。
- 看道题目我只能说出题人真会玩,斗地主都出来了。
- 这个斗地主的规则与一般的不太一样(虽然是从百度百科上粘的)。
- 看到随机数据我就松了一口气,因为这样的话不会有出题人给的神坑!!!
- 仔细分析,其实这道题没有什么完美的算法,基本确定思路:爆搜(深度优先搜索)。
- 本题花色没什么卵用,只是用来区分大小王。
- 再分析:出牌顺序不会影响出牌次数。
- 按照常规的思路,肯定要先打顺子。
- 所以就先搜顺子;注意:连着的几张牌不一定当做一个顺子一起打出,比如说6 7 8 8 9 9 10 10 J Q这组牌,如果先打出678910JQ,再打3个单牌,就不如打两个顺子678910 8910JQ更优。
- 然后出带牌,也要按照一定的顺序,比如:四带两对,四带两单,三带。
- 然后把所有不能连着出的牌统计一下,加到当前的答案中,并更新答案。
- 注意本题搜索技巧:每次进入下一步是统计一下当前牌号的种类数(因为同一号的牌一定能一下打出),并更新答案;因为A能连成顺子而2不能,所以在将牌编号时可以将3-K编号为1-11,A编号为12,2编号为13,小王为14,大王为15,这样搜的时候就会比较方便;如果有双王先打出双王,因为这样对牌局没有影响(双王不能被同时带出,但单个王可以被带出);注意利用前缀和的思想,这样可以使搜索更方便(尤其是搜顺子的时候)。
- 然后就是考验代码能力的时候了,本人蒟蒻,调了半天才调出来,代码很丑。
- 复杂度玄学,不过对于随机数据来说不成问题,期望通过本题,最慢的点300+ms。
1 var 2 t,n,i,j,x,y,anss,tt,now,ans :longint; 3 sum :Array[0..15] of longint; 4 f1,f2,f3,s1,s2,s3 :array[0..14] of longint; 5 ff :boolean; 6 7 function min(x,y:longint):longint; 8 begin 9 if x<y then exit(x) else exit(y); 10 end; 11 12 function find():longint; 13 var 14 i,summ :longint; 15 begin 16 summ:=0; 17 for i:=1 to 15 do if (sum[i]>0) then inc(summ); 18 exit(summ); 19 end; 20 21 procedure dfs(x:longint); 22 var 23 i,j,k :longint; 24 l,r,max,t,q,o :longint; 25 begin 26 q:=find(); 27 if q+x-1<anss then anss:=q+x-1;//tongji 28 {---------------------------------------------------} 29 fillchar(f1,sizeof(f1),0); 30 fillchar(s1,sizeof(s1),0); 31 for i:=1 to 12 do if (sum[i]>=3) then f1[i]:=1; 32 for i:=1 to 12 do s1[i]:=s1[i-1]+f1[i]; 33 max:=0; 34 for i:=1 to 12 do 35 for j:=i+1 to 12 do 36 if j<=l then continue; 37 if (s1[j]-s1[i-1]=j-i+1) then 38 begin 39 if (j-i+1>max) then 40 begin 41 max:=j-i+1; 42 l:=i; 43 r:=j; 44 end; 45 end; 46 if max>=2 then 47 begin 48 for i:=l to r do 49 for j:=r downto l do 50 begin 51 if j-i+1<2 then continue; 52 for k:=i to j do dec(sum[k],3); 53 dfs(x+1); 54 for k:=i to j do inc(sum[k],3); 55 end; 56 end;//san shun zi 57 {----------------------------------------------------------} 58 fillchar(f2,sizeof(f2),0); 59 fillchar(s2,sizeof(s2),0); 60 for i:=1 to 12 do if (sum[i]>=2) then f2[i]:=1; 61 for i:=1 to 12 do s2[i]:=s2[i-1]+f2[i]; 62 max:=0; 63 for i:=1 to 12 do 64 for j:=i+1 to 12 do 65 if (s2[j]-s2[i-1]=j-i+1) then 66 begin 67 if (j-i+1>max) then 68 begin 69 max:=j-i+1; 70 l:=i; 71 r:=j; 72 end; 73 end; 74 if max>=3 then 75 begin 76 for i:=l to r do 77 for j:=r downto l do 78 begin 79 if j-i+1<3 then continue; 80 for k:=i to j do dec(sum[k],2); 81 dfs(x+1); 82 for k:=i to j do inc(sum[k],2); 83 end; 84 end;//shuang shun zi 85 {--------------------------------------------------------} 86 fillchar(f3,sizeof(f3),0); 87 fillchar(s3,sizeof(s3),0); 88 for i:=1 to 12 do if (sum[i]<>0) then f3[i]:=1; 89 for i:=1 to 12 do s3[i]:=s3[i-1]+f3[i]; 90 max:=0; 91 for i:=1 to 12 do 92 for j:=i+1 to 12 do 93 if (s3[j]-s3[i-1]=j-i+1) then 94 begin 95 if (j-i+1>max) then 96 begin 97 max:=j-i+1; 98 l:=i; 99 r:=j; 100 end; 101 end; 102 if max>=5 then 103 begin 104 for i:=l to r do 105 for j:=r downto l do 106 begin 107 if j-i+1<5 then continue; 108 for k:=i to j do dec(sum[k]); 109 dfs(x+1); 110 for k:=i to j do inc(sum[k]); 111 end; 112 end;//dan shun zi 113 {--------------------------------------------------------} 114 for i:=1 to 13 do 115 begin 116 if (sum[i]=4) then 117 begin 118 dec(sum[i],4); 119 for j:=1 to 15 do 120 begin 121 if sum[j]<2 then continue; 122 for k:=j+1 to 13 do 123 begin 124 if sum[k]<2 then continue; 125 dec(sum[j],2); 126 dec(sum[k],2); 127 dfs(x+1); 128 inc(sum[j],2); 129 inc(sum[k],2); 130 end; 131 end; 132 inc(sum[i],4); 133 end; 134 end; //4 dai 2 135 {-------------------------------------------------------} 136 for i:=1 to 13 do 137 begin 138 if (sum[i]=4) then 139 begin 140 dec(sum[i],4); 141 for j:=1 to 13 do 142 begin 143 if sum[j]<>1 then continue; 144 for k:=j+1 to 15 do 145 begin 146 if sum[k]<>1 then continue; 147 dec(sum[j]); 148 dec(sum[k]); 149 dfs(x+1); 150 inc(sum[j]); 151 inc(sum[k]); 152 end; 153 end; 154 inc(sum[i],4); 155 end; 156 end; //4 dai 1 157 {---------------------------------------------------------} 158 for i:=1 to 13 do 159 begin 160 if (sum[i]=3) then 161 begin 162 dec(sum[i],3); 163 for j:=1 to 15 do 164 begin 165 if (sum[j]>2) or (sum[j]<1) then continue; 166 t:=sum[j]; 167 sum[j]:=0; 168 dfs(x+1); 169 sum[j]:=t; 170 end; 171 inc(sum[i],3); 172 end; 173 end;//san dai 1/2 174 end; 175 176 begin 177 read(t,n); 178 while (t>0) do 179 begin 180 dec(t); 181 fillchar(sum,sizeof(sum),0); 182 for i:=1 to n do 183 begin 184 read(x,y); 185 if (x>=3) then inc(sum[x-2]) else 186 if (x=1) then inc(sum[12]) else 187 if (x=2) then inc(sum[13]) else 188 if (x=0) and (y=1) then inc(sum[14]) else 189 if (x=0) and (y=2) then inc(sum[15]); 190 end; 191 ans:=0; 192 if (sum[14]>0) and (sum[15]>0) then 193 begin 194 tt:=min(sum[14],sum[15]); 195 dec(sum[14],tt); 196 dec(sum[15],tt); 197 inc(ans,tt); 198 end;//double jokers 199 anss:=maxlongint; 200 dfs(ans+1); 201 writeln(anss); 202 continue; 203 end; 204 end.