题目描述
小 A 和小 B 决定利用假期外出旅行,他们将想去的城市从 1 到 N 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i 的海拔高度为
Hi,城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值,即d[i,j] = |Hi− Hj|。旅行过程中,小 A 和小 B 轮流开车,第一天小 A 开车,之后每天轮换一次。他们计划选择一个城市 S 作为起点,一直向东行驶,并且最多行驶 X 公里就结束旅行。小 A 和小 B的驾驶风格不同,小 B 总是沿着前进方向选择一个最近的城市作为目的地,而小 A 总是沿着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的城市,或者到达目的地会使行驶的总距离超出 X 公里,他们就会结束旅行。在启程之前,小 A 想知道两个问题:
1.对于一个给定的 X=X0,从哪一个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小(如果小 B 的行驶路程为 0,此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值都最小,则输出海拔最高的那个城市。
2.对任意给定的 X=Xi和出发城市 Si,小 A 开车行驶的路程总数以及小 B 行驶的路程总数。
输入输出格式
输入格式:
第一行包含一个整数 N,表示城市的数目。
第二行有 N 个整数,每两个整数之间用一个空格隔开,依次表示城市 1 到城市 N 的海拔高度,即 H1,H2,……,Hn,且每个 Hi都是不同的。
第三行包含一个整数 X0。
第四行为一个整数 M,表示给定 M 组 Si和 Xi。
接下来的 M 行,每行包含 2 个整数 Si和 Xi,表示从城市 Si出发,最多行驶 Xi公里。
输出格式:
输出共 M+1 行。
第一行包含一个整数 S0,表示对于给定的 X0,从编号为 S0的城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比值最小。
接下来的 M 行,每行包含 2 个整数,之间用一个空格隔开,依次表示在给定的 Si和Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。
输入输出样例
drive1 4 2 3 1 4 3 4 1 3 2 3 3 3 4 3 drive2 10 4 5 6 1 2 3 7 8 9 10 7 10 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7
drive1 1 1 1 2 0 0 0 0 0 drive2 2 3 2 2 4 2 1 2 4 5 1 5 1 2 1 2 0 0 0 0 0
说明
【输入输出样例 1 说明】
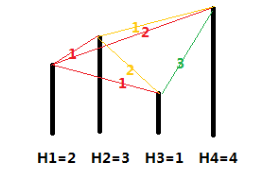
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市 1 出发,可以到达的城市为 2,3,4,这几个城市与城市 1 的距离分别为 1,1,2,但是由于城市 3 的海拔高度低于城市 2,所以我们认为城市 3 离城市 1 最近,城市 2 离城市1 第二近,所以小 A 会走到城市 2。到达城市 2 后,前面可以到达的城市为 3,4,这两个城市与城市 2 的距离分别为 2,1,所以城市 4 离城市 2 最近,因此小 B 会走到城市 4。到达城市 4 后,前面已没有可到达的城市,所以旅行结束。
如果从城市 2 出发,可以到达的城市为 3,4,这两个城市与城市 2 的距离分别为 2,1,由于城市 3 离城市 2 第二近,所以小 A 会走到城市 3。到达城市 3 后,前面尚未旅行的城市为4,所以城市 4 离城市 3 最近,但是如果要到达城市 4,则总路程为 2+3=5>3,所以小 B 会直接在城市 3 结束旅行。
如果从城市 3 出发,可以到达的城市为 4,由于没有离城市 3 第二近的城市,因此旅行还未开始就结束了。
如果从城市 4 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【输入输出样例 2 说明】
当 X=7 时,
如果从城市 1 出发,则路线为 1 -> 2 -> 3 -> 8 -> 9,小 A 走的距离为 1+2=3,小 B 走的距离为 1+1=2。(在城市 1 时,距离小 A 最近的城市是 2 和 6,但是城市 2 的海拔更高,视为与城市 1 第二近的城市,所以小 A 最终选择城市 2;走到 9 后,小 A 只有城市 10 可以走,没有第 2 选择可以选,所以没法做出选择,结束旅行)
如果从城市 2 出发,则路线为 2 -> 6 -> 7 ,小 A 和小 B 走的距离分别为 2,4。
如果从城市 3 出发,则路线为 3 -> 8 -> 9,小 A 和小 B 走的距离分别为 2,1。
如果从城市 4 出发,则路线为 4 -> 6 -> 7,小 A 和小 B 走的距离分别为 2,4。
如果从城市 5 出发,则路线为 5 -> 7 -> 8 ,小 A 和小 B 走的距离分别为 5,1。
如果从城市 6 出发,则路线为 6 -> 8 -> 9,小 A 和小 B 走的距离分别为 5,1。
如果从城市 7 出发,则路线为 7 -> 9 -> 10,小 A 和小 B 走的距离分别为 2,1。
如果从城市 8 出发,则路线为 8 -> 10,小 A 和小 B 走的距离分别为 2,0。
如果从城市 9 出发,则路线为 9,小 A 和小 B 走的距离分别为 0,0(旅行一开始就结束了)。
如果从城市 10 出发,则路线为 10,小 A 和小 B 走的距离分别为 0,0。
从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值都最小,但是城市 2 的海拔更高,所以输出第一行为 2。
【数据范围】
对于 30%的数据,有 1≤N≤20,1≤M≤20;
对于 40%的数据,有 1≤N≤100,1≤M≤100;
对于 50%的数据,有 1≤N≤100,1≤M≤1,000;
对于 70%的数据,有 1≤N≤1,000,1≤M≤10,000;
对于100%的数据,有1≤N≤100,000,1≤M≤10,000,-1,000,000,000≤Hi≤1,000,000,000,0≤X0≤1,000,000,000,1≤Si≤N,0≤Xi≤1,000,000,000,数据保证 Hi互不相同。
NOIP 2012 提高组 第一天 第三题
思路:
- 这道题双向链表+倍增也可做,不过本蒟蒻不会,所以就写了平衡树+倍增。
- 暴力模拟每次行走,暴力求出最近点和次近点,复杂度O(n^3+n^2*m),期望得分50分。
- 暴力枚举预处理出每次行走的路线,复杂度O(n*m+n^2),期望得分70分。
- 所以我们就要优化预处理和查找。
- 平衡树优化:每次查找该点两个前驱和后继,选取最近点和次近点,然后将该点插入平衡树中,复杂度O(nlogn)。
- 倍增优化:A走一步B走一步算作一步,倍增出每个点走2^i步到达的点,以及A走了多少,B走了多少,然后利用类似查询lca的方法模拟每次的路线,复杂度O(qlogn)。
- 倍增方程:f[i][j]=f[f[i-1][j-1]][j-1]; fa[i][j]=fa[i][j-1]+fa[f[i][j-1]][j-1]; fb[i][j]=fb[i][j-1]+fb[f[i][j-1]][j-1];
- 复杂度O(nlogn+qlogn),完美解决该题。
- 注意:本蒟蒻写预处理的时候没注意到海拔对最近点次近点的影响,结果过了19个点(数据较水)。。。
- 平衡树常数较大,貌似双向链表更快一些,不过本蒟蒻不会。。。
1 var 2 n,i,j,t,tot,k,k1,k2,k3,k4,x,q,s :longint; 3 a :array[-10..100050] of longint; 4 left,right,size,key :Array[0..200050] of longint; 5 next,nextt :array[-10..100050] of longint; 6 f,fa,fb :array[0..100050,0..17] of longint; 7 anspl :longint; 8 disa,disb :int64; 9 ans,cur :double; 10 11 procedure lrot(var t:longint); 12 var 13 k :longint; 14 begin 15 k:=right[t]; 16 right[t]:=left[k]; 17 left[k]:=t; 18 size[k]:=size[t]; 19 size[t]:=size[left[t]]+size[right[t]]+1; 20 t:=k; 21 end; 22 23 procedure rrot(var t:longint); 24 var 25 k :longint; 26 begin 27 k:=left[t]; 28 left[t]:=right[k]; 29 right[k]:=t; 30 size[k]:=size[t]; 31 size[t]:=size[left[t]]+size[right[t]]+1; 32 t:=k; 33 end; 34 35 procedure maintain(var t:longint; flag:boolean); 36 begin 37 if not flag then 38 begin 39 if size[left[left[t]]]>size[right[t]] then rrot(t) else 40 if size[right[left[t]]]>size[right[t]] then 41 begin 42 lrot(left[t]); 43 rrot(t); 44 end else exit; 45 end else 46 begin 47 if size[right[right[t]]]>size[left[t]] then lrot(t) else 48 if size[left[right[t]]]>size[left[t]] then 49 begin 50 rrot(right[t]); 51 lrot(t); 52 end else exit; 53 end; 54 maintain(left[t],false); 55 maintain(right[t],true); 56 maintain(t,false); 57 maintain(t,true); 58 end; 59 60 procedure insert(var t:longint; v:longint); 61 begin 62 if (t=0) then 63 begin 64 inc(tot); 65 t:=tot; 66 left[t]:=0; 67 right[t]:=0; 68 size[t]:=1; 69 key[t]:=v; 70 exit; 71 end; 72 inc(size[t]); 73 if v<key[t] then insert(left[t],v) else insert(right[t],v); 74 maintain(t,v>=key[t]); 75 end; 76 77 function pred(var t:longint; v:longint):longint; 78 var 79 k :longint; 80 begin 81 if t=0 then exit(-1); 82 if v<=key[t] then exit(pred(left[t],v)); 83 k:=pred(right[t],v); 84 if k=-1 then exit(t) else exit(k); 85 end; 86 87 function succ(var t:longint; v:longint):longint; 88 var 89 k :longint; 90 begin 91 if t=0 then exit(-1); 92 if v>=key[t] then exit(succ(right[t],v)); 93 k:=succ(left[t],v); 94 if k=-1 then exit(t) else exit(k); 95 end; 96 97 procedure find(var da,db:int64;s,x:longint); 98 var 99 i :longint; 100 p :int64; 101 begin 102 for i:=15 downto 0 do 103 begin 104 if (f[s,i]>0) and (fa[s,i]+fb[s,i]<=x) then 105 begin 106 da:=da+fa[s,i]; 107 db:=db+fb[s,i]; 108 x:=x-fa[s,i]-fb[s,i]; 109 s:=f[s,i]; 110 end; 111 end; 112 if (nextt[s]>0) and (fa[s,0]<=x) then da:=da+fa[s,0]; 113 end; 114 115 begin 116 read(n); 117 for i:=1 to n do read(a[i]); 118 for i:=n downto 1 do 119 begin 120 k1:=pred(t,a[i]); 121 k2:=succ(t,a[i]); 122 if (k1=-1) and (k2=-1) then 123 begin 124 insert(t,a[i]); 125 continue; 126 end; 127 if (k1=-1) then 128 begin 129 next[i]:=n+1-k2; 130 k3:=succ(t,a[next[i]]); 131 if (k3<>-1) then nextt[i]:=n+1-k3; 132 insert(t,a[i]); 133 continue; 134 end; 135 if (k2=-1) then 136 begin 137 next[i]:=n+1-k1; 138 k3:=pred(t,a[next[i]]); 139 if (k3<>-1) then nextt[i]:=n+1-k3; 140 insert(t,a[i]); 141 continue; 142 end; 143 if (abs(a[n+1-k1]-a[i])<=abs(a[n+1-k2]-a[i])) then 144 begin 145 next[i]:=n+1-k1; 146 k3:=pred(t,a[next[i]]); 147 if (k3=-1) or (abs(a[n+1-k3]-a[i])>abs(a[n+1-k2]-a[i])) then nextt[i]:=n+1-k2 else nextt[i]:=n+1-k3; 148 insert(t,a[i]); 149 end else 150 begin 151 next[i]:=n+1-k2; 152 k3:=succ(t,a[next[i]]); 153 if (k3=-1) or (abs(a[n+1-k3]-a[i])>=abs(a[n+1-k1]-a[i])) then nextt[i]:=n+1-k1 else nextt[i]:=n+1-k3; 154 insert(t,a[i]); 155 end; 156 end; 157 for i:=1 to n do 158 begin 159 f[i,0]:=next[nextt[i]]; 160 fa[i,0]:=abs(a[i]-a[nextt[i]]); 161 fb[i,0]:=abs(a[nextt[i]]-a[next[nextt[i]]]); 162 end; 163 for j:=1 to 15 do 164 for i:=1 to n do 165 begin 166 f[i,j]:=f[f[i,j-1],j-1]; 167 fa[i,j]:=fa[f[i,j-1],j-1]+fa[i,j-1]; 168 fb[i,j]:=fb[f[i,j-1],j-1]+fb[i,j-1]; 169 end; 170 read(x); 171 ans:=1000000000000000; 172 for i:=1 to n do 173 begin 174 disa:=0; 175 disb:=0; 176 find(disa,disb,i,x); 177 if (disb=0) then 178 begin 179 if (ans=1000000000000000) then anspl:=i else continue; 180 end else 181 begin 182 cur:=disa/disb; 183 if cur<ans then 184 begin 185 ans:=cur; 186 anspl:=i; 187 end else 188 if (cur=ans) and (a[i]>a[anspl]) then 189 begin 190 anspl:=i; 191 end; 192 end; 193 end; 194 writeln(anspl); 195 read(q); 196 for i:=1 to q do 197 begin 198 read(s,x); 199 disa:=0; 200 disb:=0; 201 find(disa,disb,s,x); 202 writeln(disa,' ',disb); 203 end; 204 end.