如果自己想要搭建一个激光相机系统,那么首要的就是要确定激光与相机的位置关系。那么下面将介绍一些典型的标定方法历史。
最早的激光相机标定方法,由一些与相机标定类似,只需要一块标定板,网站提供matlab工具包:http://www.cs.cmu.edu/~ranjith/lcct.html. 算法思路很简单,先采集十张左右的数据,分别寻找标定板在相机和激光中的对应平面方程,求解约束方程获取;两传感器位置方程。这些在作者的主页有详细介绍。


KITTI数据集的标定与这个算法类似,文章发表在2012年的ICRA上Automatic Camera and Range Sensor Calibration using a single Shot. 只不过一张图像中出现了多张标定板:
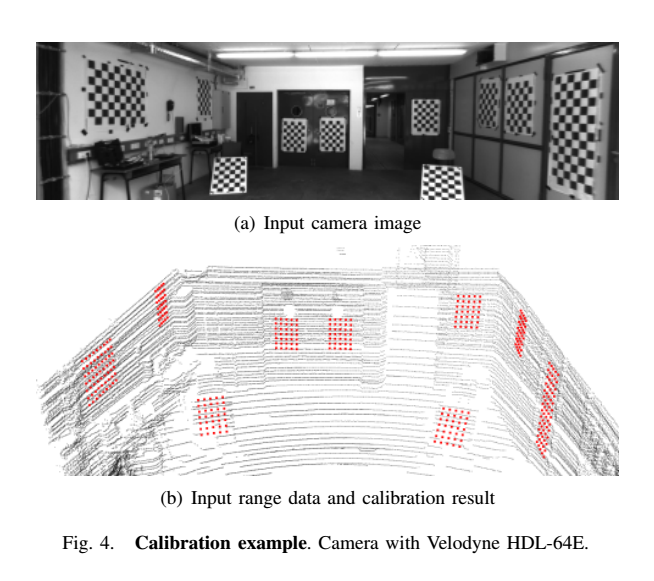
难点在作者如何对应激光中某一张的标定板就是图像上的某一张?作者利用了ransac算法,大致过程就是先假设某三个对应关系是正确的,得出相机与激光的位置关系,然后在反求其他标定板对应关系是否正确。不断循环这一操作,最终找出最优关系。
近几年又出现了,无需标定板,利用激光和图像的互信息标定:http://robots.engin.umich.edu/SoftwareData/ExtrinsicCalib.
不过笔者认为如果想要获取稳定快捷的标定方法,还是最原始的方法好。下面介绍笔者所用设备及其标定方法:

笔者所选用的是一架全景相机配合一个旋转的单线激光,单线激光的配置教程可以参考:https://jvgomez.github.io/pages/hokuyo-dynamixel-coupling-for-3d-mapping.html 其由一个hokuyo 30米激光和一个舵机dynamixel组成。通过舵机旋转,记录下每一时刻的点云来将2D激光转变为3D激光。

首先笔者对全景相机进行了标定:http://www-sop.inria.fr/icare/personnel/Christopher.Mei/ChristopherMeiPhDStudentToolbox.html. 如果是其他相机可以自行寻找标定工具包。
这个工具包都直接给出了相机的投影方程,和每个标定板在相机坐标系下的方程,我们记为:αm,i: θm,iX+dm,i=0.
另一方面利用PCL中的DoN 特征(http://pointclouds.org/documentation/tutorials/don_segmentation.php#don-segmentation)分离出标定板在激光坐标系下的方程:αl,i: θl,iX+dl,i=0.
可以通过最小化如下方程来约束RT矩阵:
$arg mathop {min }limits_{R,T} sumlimits_{i = 1}^n {frac{1}{{l(i)}}} sumlimits_{j = 1}^{l(i)} {({ heta _{m,i}}(RX_{l,i}^{(j)} + T) + {d_{m,i}})}$
R和T可以分别求解:
${{R_1} = arg mathop {max }limits_R sum heta _{c,i}^T(R{ heta _{l,i}})}$
${{t_1} = mathop {arg min }limits_t sumlimits_i {({alpha _{l,i}}} - ({alpha _{c,i}} - { heta _{c,i}}t){)^2}}$
先用USV分解求出近似解:
${R_1} = V{U^T}$
${ heta _l} heta _c^t = US{V^T}$
再用 Levenberg-Marquardt优化求解。
下面给出标定求解代码:https://github.com/ZouCheng321/6_calibration
更多详请下载我的文章:An automatic calibration between an omni-directional camera and a laser rangender for dynamic scenes reconstruction (http://ieeexplore.ieee.org/document/7866544/)
运行calibration.m 进行标定。
运行colorize.m 进行点云上色。
如果需要看上色后的效果:
cd view mkdir build cmake .. make ./cloud_viewer ../../1.pcd
可以看到图像转为3D场景:

