题目大意:
给定一棵树 每个点都有点权 每条边的长度都为1
树上一点到另一点的距离为最短路经过的边的长度总和
树上一点到另一点的花费为距离乘另一点的点权
选定一点出发 使得其他点到该点的花费总和是最大的
先dfs一遍 获得 s[u] 为u点往下的点权总和(包括u点)
由其子节点v及其本身权值可得 s[u]=s[v]+w[u]
获得 dp[u] 为u点出发往下的花费总和(u点出发的花费不需要包括u点)
由其子节点v的dp[v]及s[v]可得 dp[u]=dp[v]+s[v]
再深搜一遍树形dp 获得 dp[u] 为u点出发到其他所有点的花费总和
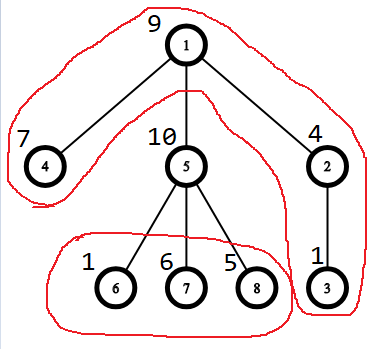
此时 fa=1 u=5
dp[fa]=dp[9]=1*(7+10+4)+2*(1+6+5+1)=(1+6+5)*2+(7+4+10)*1+1*2
dp[u]=dp[5]=1*(1+6+5+9)+2*(7+4)+3*1=(1+6+5)*1+9*1+(7+4)*2+1*3
发现由fa的结果得到u的结果需要 加上u往上的值 再减去u往下(包括u)的值
相当于 加上整棵树的值sum 再减两次u往下的值s[u] 即dp[u] = dp[fa] + sum - 2*s[u]
dp[fa]+sum-2*s[u] =(1+6+5)*2+(7+4+10)*1+1*2 + (1+6+5+7+4+10+9+1) - 2*(10+1+6+5)
=(1+6+5)*3+(7+4+10)*2+1*3+9 - 2*(10+1+6+5)
=(1+6+5)*1+(7+4)*2+1*3+9*1 = dp[u]

#include <bits/stdc++.h> #define LL long long #define INF 0x3f3f3f3f using namespace std; const int N=2e5+5; LL n, w[N]; LL ans, sum; LL s[N], dp[N]; // s[u]为u点往下的点的权值总和 vector <int> E[N]; void dfs2(int u,int fa) { if(fa) dp[u]=dp[fa]+sum-2*s[u]; // 如果u存在父节点 由dp[fa]可得到dp[u] // 此时dp[u]为由u点出发去往其他所有点的总花费 for(int i=0;i<E[u].size();i++) { int v=E[u][i]; if(v==fa) continue; dfs2(v,u); } ans=max(ans,dp[u]); } void dfs1(int u,int fa) { s[u]=w[u]; for(int i=0;i<E[u].size();i++) { int v=E[u][i]; if(v==fa) continue; dfs1(v,u); s[u]+=s[v]; dp[u]=dp[u]+dp[v]+s[v]; // 此时dp[u]为由u点出发往下的总花费 } } int main() { while(~scanf("%I64d",&n)) { ans=sum=0LL; for(int i=1;i<=n;i++) { scanf("%I64d",&w[i]); sum+=w[i]; E[i].clear(); } for(int i=1;i<n;i++) { int u,v; scanf("%d%d",&u,&v); E[u].push_back(v); E[v].push_back(u); } memset(s,0,sizeof(s)); memset(dp,0,sizeof(dp)); dfs1(1,0); dfs2(1,0); printf("%I64d ",ans); } return 0; }
