在互联网时代,经常会有产生【随机数】的应用场景。
比如说最常见的团购业务,用户购买一张团购券,然后客户的手机中会接收到一个随机的团购码。客户拿着这个团购码去门店验证消费。
相面大家都对上面的这种方式比较熟悉。如果站上技术的角度,我们来分析一下这个【团购码】其实还是有很多细节在里面的。接下来我们来对这部分细节进行探讨。
假设用点击领用团购码,产生一个10000 以内的随机数。该数字发到用户手机上,作为验证凭证。
那么这个团购码需要满足下面的几个条件:
1:每次都是随机产生,用户不能轻易猜测到下一个验证码。
2:团购码的数值范围必需【00001,10000】。——实际中这个数字会比较大。
3:用户领用的团购码是决对唯一的,即产生的每个数字,只会出现一次。不会存在多个用户领用同一个验证码的情况。
上面条件的技术难点在于如何生成不重复的随机数?
大家知道,一般我们用的编程语言所提供的随机数方法,都不能保证下一次的随机数和前面的不重复。即我们生成了100个随机数里面,就可能会有N个是重复。
那么如何保证其不重复性? 很容易想到的方案是,每次生成一个新的随机数后,再去和前面的所有的随机数进行比较,如果重复则抛弃。
但是这样做好么?假设要生成1000个随机数,每次都和前面的进行比较好像问题不大。要是要1亿的范围呢?
我有个朋友正好在一家知明的团购公司工作,我向他了解下他们公司生成团购码的方法。
总体思路是:
1:生成一批待用的码放在码池中。用的是编程语言所提供的随机数方法。
2:用户领用码后,生成一条领用记录,并且码池中除非该码。
3:定期检查码池,生成新的码放入池中。
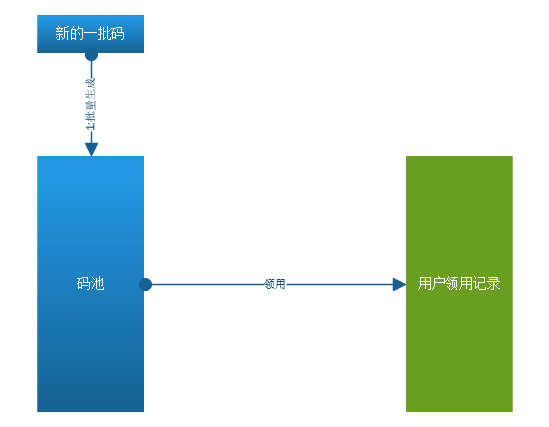
同样面临重复码的问题。如果两个用户a,b 在不同时间段领到了相同的团购码。用户a 比用户 b 更先一步去门店消费,然后更新该团购码的状态。那么用户b的那个码也会更新,则用户b来消费的时候会发现该码已经被用了。
他们如何解决这个问题,在步骤1 批量生成码的时想,先check码池的所有记录是否重复。当然最好再和用户领用记录check一下。
这样会带来性能上的很大消耗。或许可以想一些办法可以减少这方面的损失,比如码池放更多的码,过期的领用的记录及时清理。
更多的具体细节,不再去深入。
上面的做法,多多少少不是很理想。没有在关键点上解决问题——用一种算法每次生成一个和前面不重复的随机数。
基于上述类似场景,提供一个《线性同余产生随机数》算法,每次生成一个不重复的随机数。
算法参考:http://www.asmedu.net/algorithm.jsp?index=46
线性同余产生随机数算法解析:
Xn+1 = ( a * Xn + c ) mod m ,n >= 0
其中: 0 < m ;0 <= a<m ; 0 <=c<m
开始指定一个X0( 0<=X0<m ),依赖上次的值Xn,每次得到一个数Xn+1。根据这个算法所求的随机数序列{X0,X1,...Xn},称作线性同余序列。
同余序列总是进入一个循环,它最终必定在n个数之间无休止的重复循环。它的最大循环周期为m。
得到最大的周期m的条件如下:
(1)c与m为互质数。
(2)对于整除m的每个素数p,b=a-1是p的倍数。
(3)如果m是4的倍数,则b也是4的倍数。
以取10000个 随机数为例,m = 10000;按最大的周期条件设定c = 3; a = 21; x0=4。
代码如下:
1 public static void RandomGenerator(ref long previousVaule) 2 { 3 //Xn+1 = ( aXn + c ) mod m ,n >= 0 4 long m = 10000L; 5 long c = 3L; 6 long a = 21L; 7 8 previousVaule = (a * previousVaule + c) % m; 9 }
long ab = 4; HashSet<long> hash = new HashSet<long>(); for (int i = 0; i < 10000; i++) { RandomGenerator(ref ab); hash.Add(ab); Console.WriteLine(ab); } Console.WriteLine("总数:"+hash.Count);
运行结果:
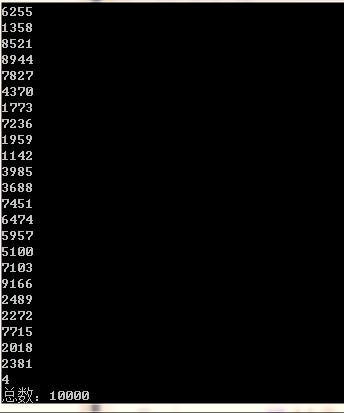
经测试可以验证,10000次随机将穷举所有< 10000的数字不会发生重复。现实应用中,还要解决分布式情况下,对上次的值Xn依赖的争用问题。
最后,大家可能还是有疑问。这样的随机码冒似可以破解。这批随机码是有规率的对吗?
所以最后对每次批量生成的码,要再把它们的顺序打乱一下再存到池中。
最重要的是下批量生成的码将不会和前面的重复。