题意: 把 n 个数分成若干组,组内互质,问最少要分几组。题目给 了一个贪心的假算法,你需要构造一组输入和对应的解使得你分的 组数恰好比贪心的少 k ,不要求你分的也是最少的
数组a不能有重复元素的解法
给定数组A,要求将A分最少的组,每组内的元素互质 有一个假算法,枚举A[1..n],如果没有可加入的组就新建一个组,反之加入那个组 构造一组数据使得该算法错误 构造:令每个数都对应一个顶点,如果两个点u,v不互质, 就在这两个点之间连接一条边,边权是gcd(u,v) 问题就转化成了构造一张图,按假算法的染色方案是x种颜色,但是存在一种x-k的染色方案 用二分图的性质来构造,肯定存在一种染色数是2的方案(二分图左右两侧) 于是要构造一种连边的方案,让假算法的染色方案结果是2+k 由于k=7,所以我们只要构造出染色是9的情况就行 构造出图后,给每条边权都赋值为一个不同的质数,然后点权为所有和它相连的边权乘积

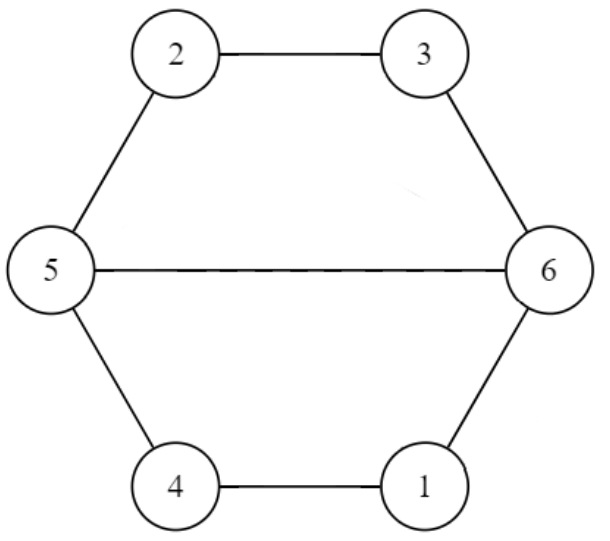
当然这题没有这个限制(据说出题人(忘加了) ,所以就是很简单的把答案复读k次就行。。