求整数数组中和最大的子数组

合作队员：张硕——李帅

      同样是星期一，同样是10:10——12：00的软件工程课，同样是带电脑上课，这节课的主要内容是代码的规范和结对项目开发，在结对项目开发中，两个人的角色可以用驾驶员和领航员来代替，然而驾驶员和领航员的角色是可以互换的，这就需要两个人对项目开发的思路达成共识，一个人写代码，另外一个人在一旁指导可以发现对方在写代码时有哪些错误，并可以以正确的方式向对方提出。当两个人换角色之后，依然可以行云流水的将代码写完，达到一定的默契。好了，切入正题：

      输入一个整型数组，数组里有正数也有负数。数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。求所有子数组的和的最大值。要求时间复杂度为O(n)。

      下面整理一下我们上课的思路：

      假设整型数组中有n个数，那么若想找到数组中连续的一个或者多个整数的和最大的那个子数组，(切不要忘记一个数的时候)那么就要利用循环从第一个数开始加，先定义一个最大值max，这就又涉及到最大值的初始化，令max=list[0]，即数组中第一个元素，之后加后边的一个元素，得到的sum和max进行比较。继续用sum加相邻后边的一个元素，（实际上就是从第一个数开始计算它本身时的值，然后再计算从它开始的两个数的和，三个数的和。。。。）加一次进行一次比较。i=0比较结束，i=1继续按照这个思路进行比较。这样就不会遗漏掉每一个子数组，（当然时间复杂度就不会达到要求了）最后返回最大值即可。

       但是我们开始写代码时，帅哥想到了用递归函数，此时紧张的心情已将顾忌不到时间复杂度的问题了。所以时间就浪费了，导致课上没有弄出来。

int max(int list[],int length)
{
    int sum ;
    int i,j;
    int max = list[0];
    for(i = 0; i<length; i++)
    {
        sum=0;
        for(j = i;j<length; j++)
        {
            sum=sum+list[j];
            if(sum>max)
            {
                max = sum;
            }
        }
    }
    return max;
}

当然这个算法的时间复杂度并没有达到要求O(n)，而是0（n^2）,下面是整个程序的代码：

#include<iostream>
#define maxnum 1000
using namespace std;
int max(int list[],int length)
{
    int sum ;
    int i,j;
    int max = list[0];
    for(i = 0; i<length; i++)
    {
        sum=0;
        for(j = i;j<length; j++)
        {
            sum=sum+list[j];
            if(sum>max)
            {
                max = sum;
            }
        }
    }
    return max;
}
int main()
{
    int array[maxnum];
    int n;
    cout<<"请输入数组的长度:"<<endl;
    cin>>n;
    cout<<"请输入相关的数据："<<endl;
    for(int i=0;i<n;i++)
    {
        cin>>array[i];
    }
    cout<<"数组中最大的子数组的和为："<<max(array,n)<<endl;
    return 0;
}

测试结果：

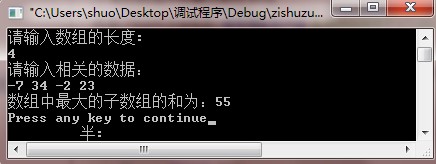
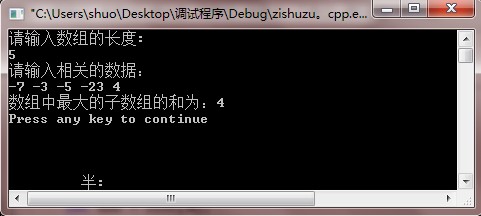
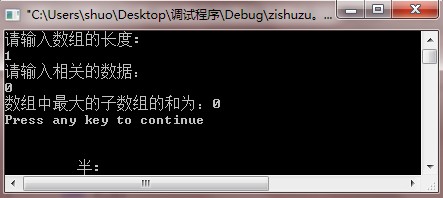
时间复杂度为O(n)的算法还在进一步研究中。。。

另外附上课上思路草稿：