网络瘤,顾名思义,就是网上的毒瘤题用来求网络中的流量(_{_{_ ext等}})的算法。
实现方法
电风扇dfs
名词解释
- 源点:水流的出发点
- 汇点:水流的终点
- 流量:流过一条边(点)的水量
- 容量:一条边(点)能装下的最大水量
- 增广路(与二分图不同):从源点到汇点的一条路径,路径上每一条边的流量<容量
思路
-
最大流
- 考虑用dfs来找增广路,每找到一条就往里面灌满水,直到找不到为止。
- 这种做法明显是错误的,比如下面的图
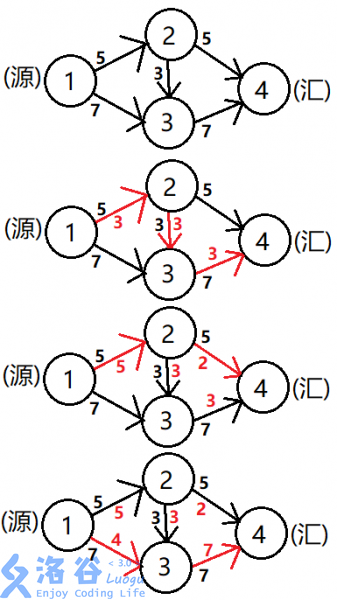
- 此时流量为9,而最大流为12
- 考虑记录每一条边还可以流过的水量为残量
- 如上图,(1 o3)的残量为3,(2 o3)的残量为0;
- 而(3 o2)的残量为3(相当于从3最多可以有3个单位的水流回2)
- 于是更新增广路的定义为:从源点到汇点的一条路径,路径上每一条边的残量>0
- 不难发现,上图中还有一条增广路为(1 o3 o2 o4),容量刚好为3
- 于是对每一条边建一条反边,初始残量为0,之后保证边(e)与它的反边(e')残量之和为(e)的初始残量
- 附上代码:
int Last[10002],Next[1000002],dis[10002],End[1000002],tot=1,cnt[10002];
int End_point,;
long long Len[1000002],ans=0;
long long dfs(int p,long long maxx)
{
if(p==End_point)return maxx;
long long cntt=0,val;
int i=Last[p];
while(i)
{
if(Len[i]&&dis[End[i]]==dis[p]-1)
{
val=dfs(End[i],Min(Len[i],maxx-cntt));
Len[i]-=val;
Len[i^1]+=val;
cntt+=val;
if(cntt==maxx||dis[1]>=tot)return cntt;
}
i=Next[i];
}
if(dis[1]>=tot)return cntt;
if((--cnt[dis[p]++])==0)dis[1]=tot;
cnt[dis[p]]++;
return cntt;
}
剩余部分见费用瘤(咕咕中)