题目描述
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中,牌的大小关系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
具体规则如下:
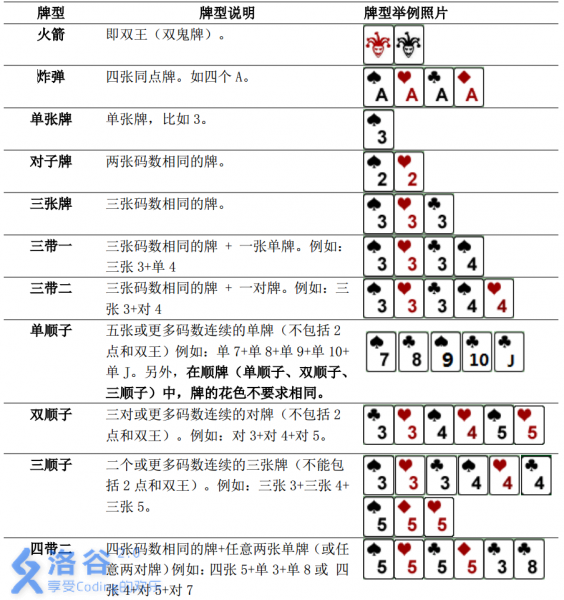
输入输出格式
输入格式:第一行包含用空格隔开的2个正整数T和n,表示手牌的组数以及每组手牌的张数。
接下来T组数据,每组数据n行,每行一个非负整数对aibi表示一张牌,其中ai示牌的数码,bi表示牌的花色,中间用空格隔开。特别的,我们用1来表示数码A,11表示数码J,12表示数码Q,13表示数码K;黑桃、红心、梅花、方片分别用1-4来表示;小王的表示方法为01,大王的表示方法为02。
输出格式:共T行,每行一个整数,表示打光第i手牌的最少次数。
输入输出样例
输入样例#1:
1 8 7 4 8 4 9 1 10 4 11 1 5 1 1 4 1 1
输出样例#1:
3
输入样例#2:
1 17 12 3 4 3 2 3 5 4 10 2 3 3 12 2 0 1 1 3 10 1 6 2 12 1 11 3 5 2 12 4 2 2 7 2
输出样例#2:
6
说明
样例1说明
共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
对于不同的测试点, 我们约定手牌组数T与张数n的规模如下:
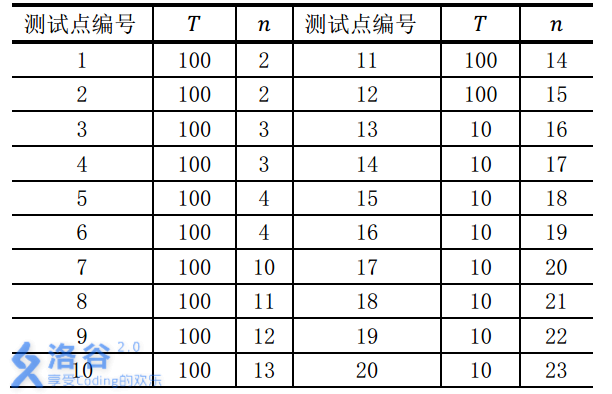
数据保证:所有的手牌都是随机生成的。
dp+深搜版
1 8
3 1
3 2
3 3
5 1
5 2
5 3
8 1
8 2
8 3
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 using namespace std; 6 const int MAXN=24; 7 int T,n,p,hs,ans; 8 int dp[MAXN][MAXN][MAXN][MAXN],card_num[MAXN],happen[MAXN/4]; 9 int take_num[5]={0,5,3,2}; 10 int read(int & n) 11 { 12 char c='-';int x=0; 13 while(c<'0'||c>'9')c=getchar(); 14 while(c>='0'&&c<='9') 15 { 16 x=x*10+(c-48); 17 c=getchar(); 18 } 19 n=x; 20 } 21 int calc(int one,int two,int three,int four,int king) 22 { 23 if(king==1)// 只有一张大小王 24 { 25 one++;// 看做单牌处理 26 king=0; 27 } 28 if(king==0) 29 return dp[four][three][two][one]; 30 else 31 return min(dp[four][three][two][one+2],dp[four][three][two][one]+1); 32 } 33 void dfs(int now)//now是指已经操作的次数 34 { 35 if(now>ans) 36 return ; 37 memset(happen,0,sizeof(happen));// 初始化 38 for(int i=2;i<=14;i++) 39 happen[card_num[i]]++; 40 ans=min(ans,now+calc(happen[1],happen[2],happen[3],happen[4],card_num[0])); 41 for(int k=1;k<=3;k++)// 顺子 42 { 43 for(int i=3;i<=14;i++) 44 { 45 int j; 46 for(j=i;j<=14&&card_num[j]>=k;j++) 47 { 48 card_num[j]-=k; 49 if(j-i+1>=take_num[k]) 50 dfs(now+1); 51 } 52 for(j--;j>=i;j--) 53 card_num[j]+=k; 54 } 55 } 56 } 57 int main() 58 { 59 // freopen("landlords.in","r",stdin); 60 // freopen("landlords.out","w",stdout); 61 read(T);read(n); 62 memset(dp,1,sizeof dp); 63 dp[0][0][0][0]=0; 64 // dp[i][j][k][l]表示打出i套四张,j套三张,k套两站,l张单牌所需要的最少步数 65 for(int i=0;i<=n;i++)//四张 66 for(int j=0;j<=n;j++)//三张 67 for(int k=0;k<=n;k++)//两张 68 for(int l=0;l<=n;l++)//一张 69 if(i*4+j*3+k*2+l*1<=n) 70 { 71 dp[i][j][k][l]=i+j+k+l;//最坏的情况 72 if(i) 73 { 74 if(k>=2) 75 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k-2][l]+1); 76 // 四带一对对牌 77 if(l>=2) 78 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k][l-2]+1); 79 // 一对单牌 80 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k][l]+1); 81 //啥都不带 82 } 83 if(j) 84 { 85 if(k) 86 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k-1][l]+1); 87 // 3带对 88 if(l) 89 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k][l-1]+1); 90 // 3带单 91 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k][l]+1); 92 // 什么都不带 93 } 94 if(k) 95 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j][k-1][l]+1); 96 if(l) 97 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j][k][l-1]+1); 98 } 99 while(T--) 100 { 101 memset(card_num,0,sizeof(card_num));// 初始化 102 ans=n; 103 for(int i=1;i<=n;i++) 104 { 105 read(p);read(hs); 106 if(p==0) 107 card_num[0]++;//大小王 108 else if(p==1) 109 card_num[14]++;// A 110 else card_num[p]++; 111 } 112 dfs(0); 113 printf("%d ",ans); 114 } 115 return 0; 116 }