题目描述
一条单向的铁路线上,依次有编号为 1, 2, …, n 的 n 个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。
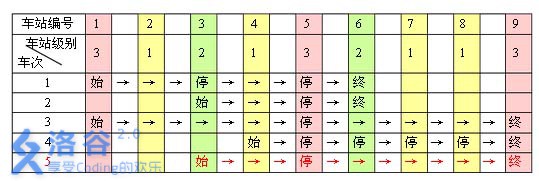
现有 m 趟车次的运行情况(全部满足要求),试推算这 n 个火车站至少分为几个不同的级别。
输入输出格式
输入格式:输入文件为 level.in。
第一行包含 2 个正整数 n, m,用一个空格隔开。
第 i + 1 行(1 ≤ i ≤ m)中,首先是一个正整数 si(2 ≤ si
≤ n),表示第 i 趟车次有 si 个停靠站;接下来有 si个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式:输出文件为 level.out。
输出只有一行,包含一个正整数,即 n 个火车站最少划分的级别数。
输入输出样例
9 2 4 1 3 5 6 3 3 5 6
2
9 3 4 1 3 5 6 3 3 5 6 3 1 5 9
3
说明
对于 20%的数据,1 ≤ n, m ≤ 10;
对于 50%的数据,1 ≤ n, m ≤ 100;
对于 100%的数据,1 ≤ n, m ≤ 1000。
思路我就不多说了,不懂的可以参考楼下,就是建边+拓扑排序
我来解答一下讨论区的疑问
一.8.9.10这三个点莫名RE,那么请开一个map数组,记录两条边之间有没有路径相连,相当于一个访问标记
二.第2、8点TLE ,检查一下你的读入时候的枚举,必须要先枚举开始和结束的所有点,然后满足条件的话再暴力建边
三.还是TLE ,请把你的map数组改成bool类型!!!!!!!!!!!!!!!
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 void read(int & n) 9 { 10 char c='+';int x=0;int flag=0; 11 while(c<'0'||c>'9') 12 { 13 c=getchar(); 14 if(c=='-') 15 flag=1; 16 } 17 while(c>='0'&&c<='9') 18 x=x*10+(c-48),c=getchar(); 19 flag==1?n=-x:n=x; 20 } 21 const int MAXN=1001; 22 struct node 23 { 24 int u,v,nxt; 25 }edge[1000001]; 26 int head[MAXN]; 27 int num=1; 28 int n,m,p,gg; 29 int a[MAXN]; 30 int vis[MAXN]; 31 int rudu[MAXN]; 32 int step[MAXN]; 33 bool map[MAXN][MAXN]; 34 inline void add_edge(int x,int y) 35 { 36 edge[num].u=x; 37 edge[num].v=y; 38 edge[num].nxt=head[x]; 39 head[x]=num++; 40 } 41 inline void init() 42 { 43 read(n);read(m); 44 for(int i=1;i<=n;i++)head[i]=-1; 45 for(int i=1;i<=m;i++) 46 { 47 memset(vis,0,sizeof(vis)); 48 read(p); 49 for(int i=1;i<=p;i++) 50 { 51 read(a[i]); 52 vis[a[i]]=1; 53 } 54 for(int i=1;i<=p;i++) 55 for(int j=a[1];j<=a[p];j++) 56 if(vis[j]==0&&map[a[i]][j]==0) 57 { 58 add_edge(a[i],j); 59 map[a[i]][j]=1; 60 rudu[j]++; 61 } 62 } 63 } 64 inline void Topsort() 65 { 66 queue<int>q; 67 for(int i=1;i<=n;i++) 68 if(rudu[i]==0) 69 q.push(i); 70 int ans=0; 71 while(q.size()!=0) 72 { 73 int p=q.front(); 74 q.pop(); 75 for(int i=head[p];i!=-1;i=edge[i].nxt) 76 { 77 rudu[edge[i].v]--; 78 if(rudu[edge[i].v]==0) 79 { 80 q.push(edge[i].v); 81 step[edge[i].v]=step[edge[i].u]+1; 82 ans=max(ans,step[edge[i].v]); 83 } 84 } 85 } 86 printf("%d",ans+1); 87 } 88 int main() 89 { 90 init(); 91 Topsort(); 92 return 0; 93 }