无向图的强连通分量

 

本篇博客存在非常大的概念上的错误(算法没有错误)

更正的版本在这里

http://www.cnblogs.com/zwfymqz/p/8480552.html

http://www.cnblogs.com/zwfymqz/p/8480429.html

对此，我表示深深地抱歉

在学习无向图的强联通分量之前

你首先要明白有向图的强联通分量 

 

以前的自己too naive ，这玩意儿其实叫边双联通分量QWQ。。

 

定义

对于任意两个点，如果存在至少两条互相不重合的路径，使得这两点可以相互到达，那么这两个点就属于同一个强联通分量

比如说

 

 

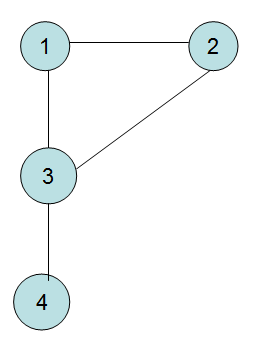
 在这张图中，

$1,2,3$属于一个强联通分量

$4$属于一个强联通分量，因为$3,4$只有一条可以相互到达的路径

 

 

实现

和有向图的强联通分量类似

都是用Tarjan算法实现

在求无向图的强联通分量重，我们不允许走已经走过的边

所以我们在Tarjan的过程中还需要记录一个father

走的时候只能走目标节点不是father的点

int Tarjan(int now,int fa)
{
	dfn[now]=low[now]=++tot;
	vis[now]=1;
	s.push(now);
	for(int i=head[now];i!=-1;i=edge[i].nxt)
	{
		if(dfn[edge[i].v]==0)	
			Tarjan(edge[i].v,now),low[now]=min(low[now],low[edge[i].v]);
		else if(vis[edge[i].v]&&edge[i].v!=fa)	
			low[now]=min(low[now],dfn[edge[i].v]);
	}
	if(dfn[now]==low[now])
	{
		int top;
		++colornum;
		do
		{
			top=s.top();	color[top]=colornum;
			vis[top]=0;	s.pop();
		}while(top!=now);
	}
}

 

 

例题

放一道我们考试的题目

 　

题解点这里
向下翻到第三题