| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 9762 | Accepted: 4397 |
Description
Consider the two networks shown below. Assuming that data moves around these networks only between directly connected nodes on a peer-to-peer basis, a failure of a single node, 3, in the network on the left would prevent some of the still available nodes from communicating with each other. Nodes 1 and 2 could still communicate with each other as could nodes 4 and 5, but communication between any other pairs of nodes would no longer be possible.
Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.
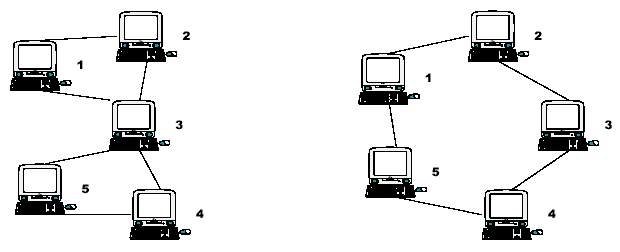
Node 3 is therefore a Single Point of Failure (SPF) for this network. Strictly, an SPF will be defined as any node that, if unavailable, would prevent at least one pair of available nodes from being able to communicate on what was previously a fully connected network. Note that the network on the right has no such node; there is no SPF in the network. At least two machines must fail before there are any pairs of available nodes which cannot communicate.

Input
The input will contain the description of several networks. A network description will consist of pairs of integers, one pair per line, that identify connected nodes. Ordering of the pairs is irrelevant; 1 2 and 2 1 specify the same connection. All node numbers will range from 1 to 1000. A line containing a single zero ends the list of connected nodes. An empty network description flags the end of the input. Blank lines in the input file should be ignored.
Output
For each network in the input, you will output its number in the file, followed by a list of any SPF nodes that exist.
The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.
The first network in the file should be identified as "Network #1", the second as "Network #2", etc. For each SPF node, output a line, formatted as shown in the examples below, that identifies the node and the number of fully connected subnets that remain when that node fails. If the network has no SPF nodes, simply output the text "No SPF nodes" instead of a list of SPF nodes.
Sample Input
1 2 5 4 3 1 3 2 3 4 3 5 0 1 2 2 3 3 4 4 5 5 1 0 1 2 2 3 3 4 4 6 6 3 2 5 5 1 0 0
Sample Output
Network #1 SPF node 3 leaves 2 subnets Network #2 No SPF nodes Network #3 SPF node 2 leaves 2 subnets SPF node 3 leaves 2 subnets
Source
题意:
给你一张图,问哪些点是割点,并输出去掉割点之后有几个联通快
这题直接有毒啊。
思维难度:☆
算法实现难度:☆
数据读入输出处理难度:☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
思路比较简单,tarjan求割点的时候统计一下出度
对于每次tarjan的根节点特判一下
因为题目保证图联通,因此只需要判断一即可
设ans[x]为第x个点的答案
若x==1 则输出ans[x]
否则为ans[x]+1 (这个点上面还有一坨点)
因为我们已经对根进行了限制,所以tarjan的时候就不需要记录根节点了
// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<algorithm> //#define getchar() (S == T && (T = (S = BB) + fread(BB, 1, 1 << 15, stdin), S == T) ? EOF : *S++) //char BB[1 << 15], *S = BB, *T = BB; using namespace std; const int MAXN=1e5+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } struct node { int u,v,nxt; }edge[MAXN]; int head[MAXN],num=1; inline void AddEdge(int x,int y) { edge[num].u=x; edge[num].v=y; edge[num].nxt=head[x]; head[x]=num++; } int low[MAXN],dfn[MAXN],ans[MAXN],tot=0,N; void tarjan(int now) { dfn[now]=low[now]=++tot; int ch=0; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]) { tarjan(edge[i].v); low[now]=min(low[now],low[edge[i].v]); if(low[edge[i].v]>=dfn[now]) ans[now]++; } else low[now]=min(low[now],dfn[edge[i].v]); } } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif int cur=0; while(1) { memset(head,-1,sizeof(head)); memset(ans,0,sizeof(ans)); memset(low,0,sizeof(low)); memset(dfn,0,sizeof(dfn)); num=1; bool flag=1; int x,y; while(1) { scanf("%d",&x); if(x==0) break; flag=0; scanf("%d",&y); AddEdge(x,y);AddEdge(y,x); N=max(N,max(x,y)); } if(flag==1) break; tarjan(1); flag=1; printf("Network #%d ",++cur); if(ans[1]>1) printf(" SPF node %d leaves %d subnets ",1,ans[1]),flag=0; for(int i=2;i<=N;i++) if(ans[i]>=1) printf(" SPF node %d leaves %d subnets ",i,ans[i]+1),flag=0; if(flag==1) printf(" No SPF nodes "); putchar(' '); } return 0; }