模数的世界[数论]

模数的世界[数论]

题解：

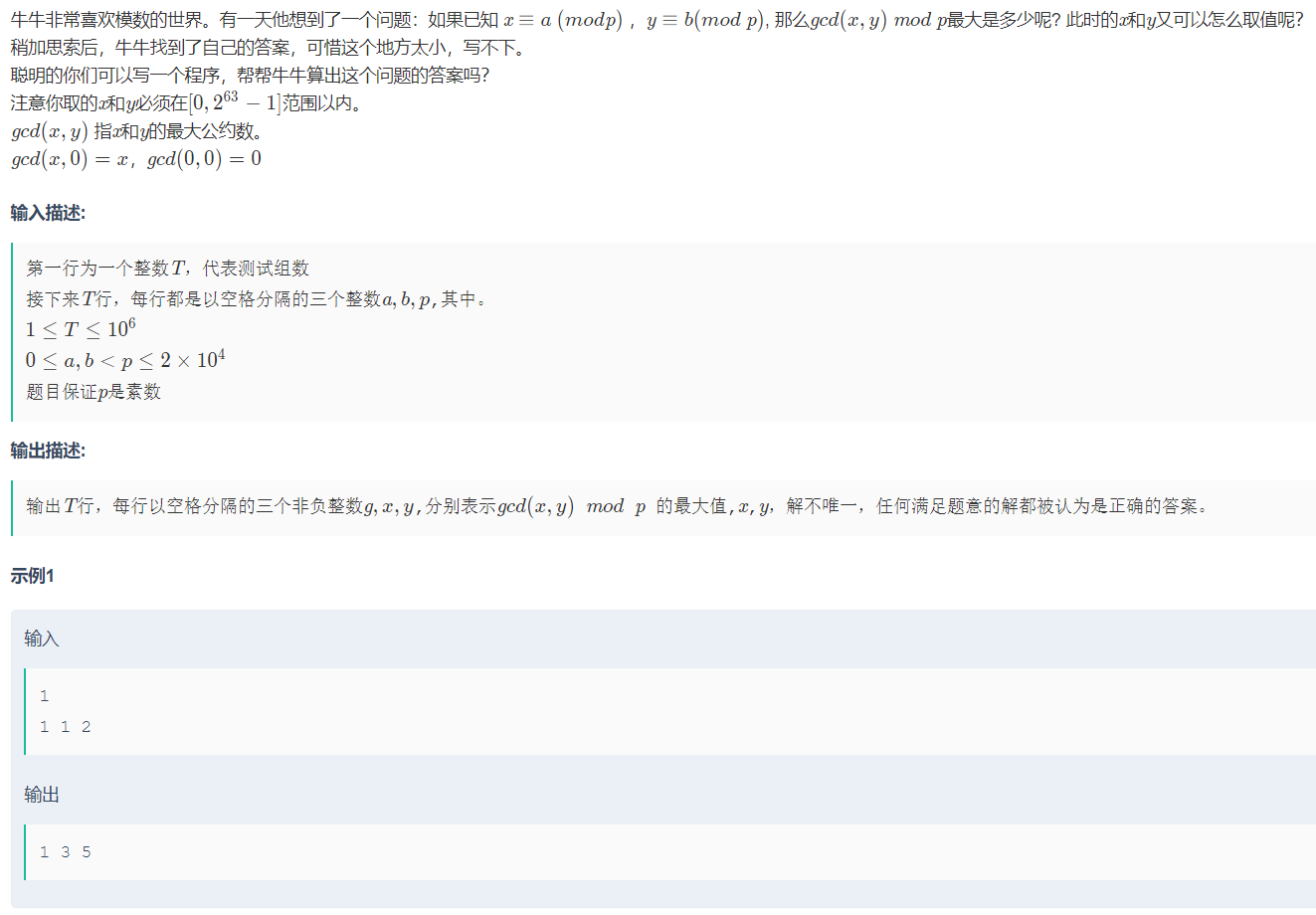
\[\begin{align} &要使gcd(x,y)=gcd(Ap+a,Bp+B)=p-1\Rightarrow p-1|Ap+a,\quad p-1|B+b ,\quad gcd((Ap+a)/(p-1),(Bp+b)/(p-1))=1\\ &构造Ap+a=(k1*p-a)(p-1),\quad Bp+b=(k1*p-b)(p-1),则要使gcd(k1*p-a,k2*p-b)=1\\ &不妨令k2=1，则下面证明 必然存在k1\in[1,c] ,\quad s.t. gcd(k1*p-a,p-b)=1\\ &令c=p-b\\ &首先,\forall k1,k2 \in [1,c],\quad k1*p-a\not =k2*p-a(mod\quad c) [反证法]\\ & \therefore \exist k1,s.t.k1*p-a=1 (mod \quad c) \\ &根据辗转相除,gcd(ac+1，c)=1\\ &\therefore ,必然存在k1\in[1,c] ,\quad s.t. gcd(k1*p-a,p-b)=1 \end{align} \]

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define debug(x) cout<<#x<<':'<<x<<endl;
int T;
/*
x=(k1*p-a)(p-1),y=(p2*b-p)(p-1)
gcd(k1*p-a,k2*p-b)=1; 
令k2=1,枚举k1

*/
int main(){
    scanf("%d",&T);
    cout<<__gcd(0,3)<<endl;
    ll a,b,p,x,y;
    while(T--){
        scanf("%lld%lld%lld",&a,&b,&p);
        if(a==0&&b==0){//p|gcd(x,y)
            printf("0 0 0\n");
            continue;
        }
        else if(__gcd(p-a,p-b)==1){
            printf("%lld %lld %lld\n",p-1,(p-1)*(p-a),(p-1)*(p-b));
        }
        else {
            printf("%lld %lld %lld\n",p-1,(2*p-1)*(p-a),(p-1)*(p-b));
        }
        

    }
    
}