链表
链表的底层实现
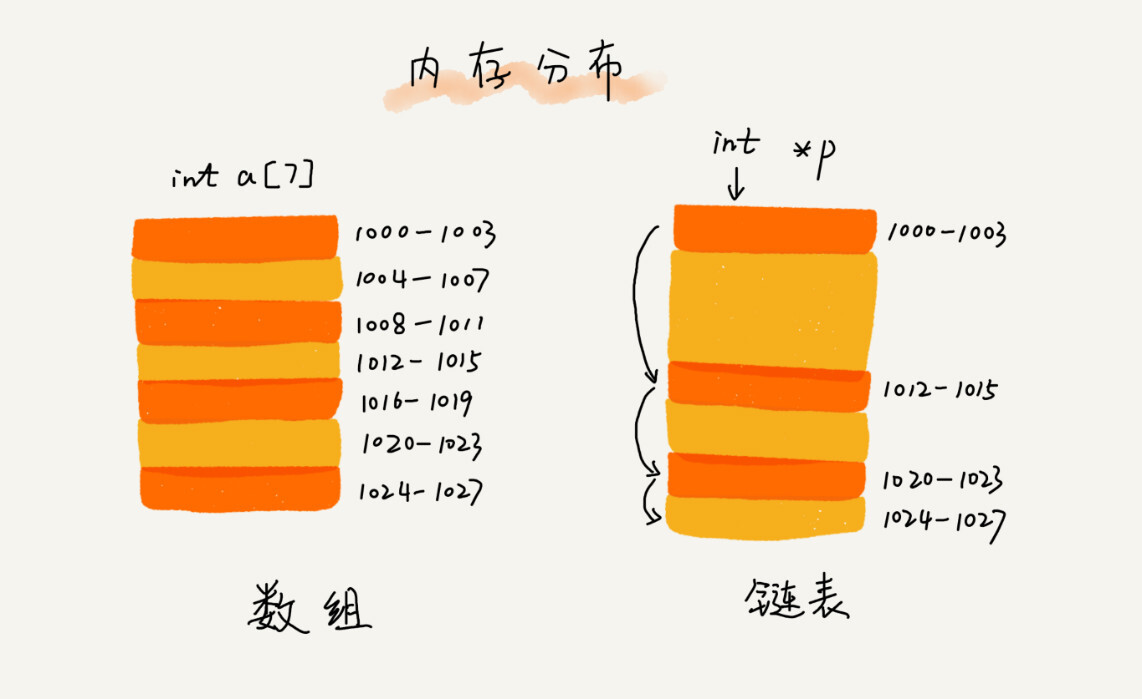
数组是连续的内存空间,所以内存是必需连续的,但是,链表它是通过指针将一组零散的内存块串联起来使用的。
指针可以保存地址值(指针)的变量称为指针变量,因为指针变量中保存的是地址值
假如
硬盘最后就剩下100M的内存了,如果剩下的这100M是一块完整的内存,那么就可以声明一个100M的数组,但是链表的要求就没有那么多。但是相反的链表使用的内存会更多,因为它存储这下一个数据的指针。
单链表
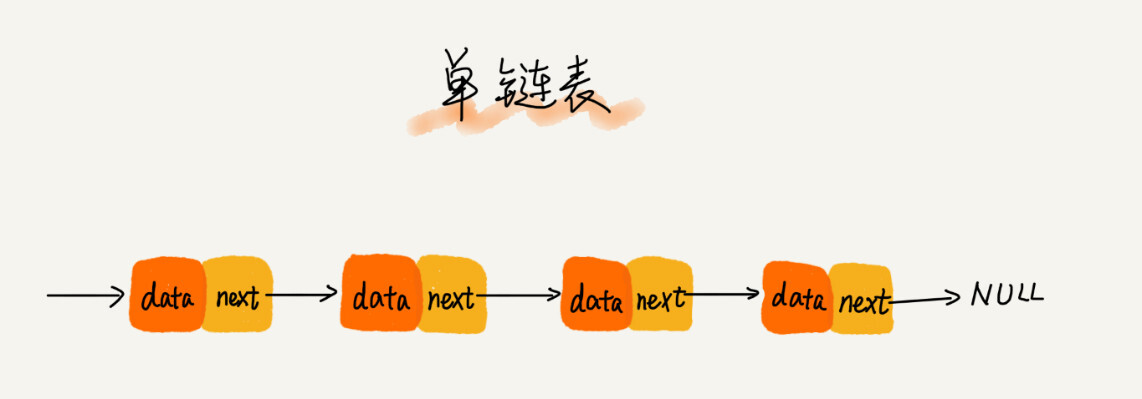
链表通过指针将一组零散的内存块串联到一起。其中的内存块我们称为结点Node,结点中不仅存储着数据,还有下一个结点的地址,这个结点地址称为后继指针next
第一个结点称为头结点,最后一个称为尾结点,尾结点指向为空地址null
时间复杂度分析
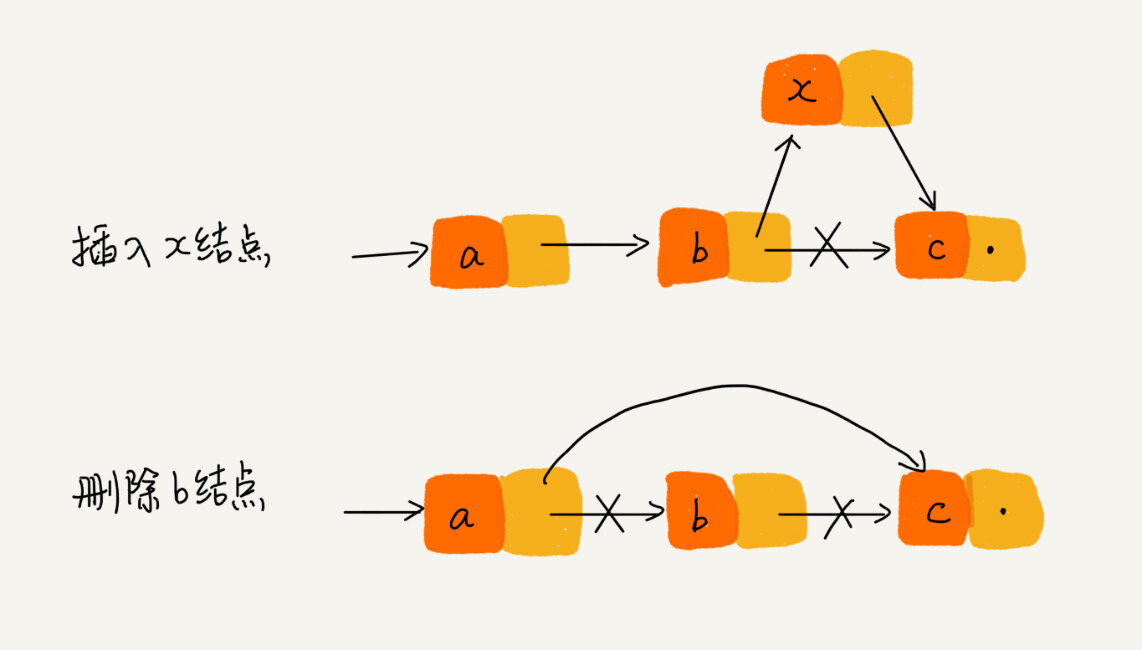
插入数据,删除数据
O(1),只要改变结点的后继指针指向就行了
查询数据
O(n)由于内存地址不是连续的,所以不能使用例如数组的那一套,求址算法,只能从头一个一个的去找
循环链表
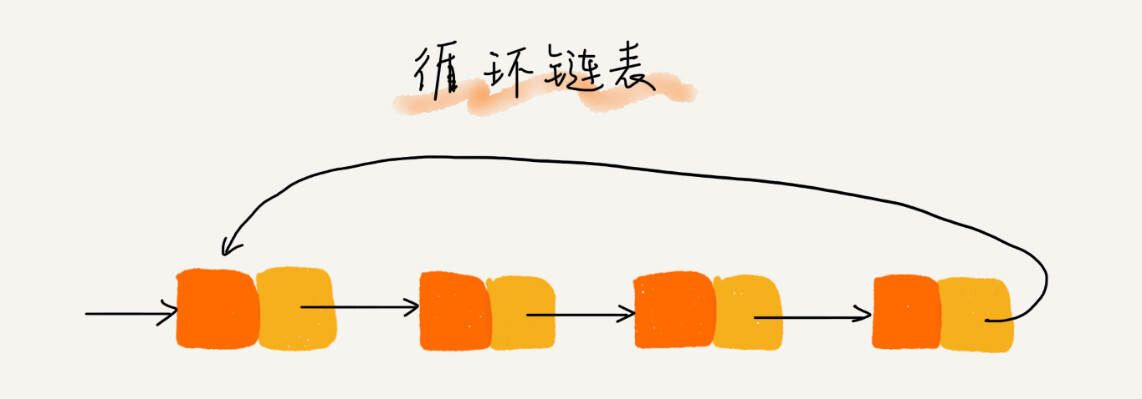
循环链表是一种特殊的单链表,就是把尾结点的后继指针指向第一个结点,实现了循环的效果
时间复杂度和单链表一样
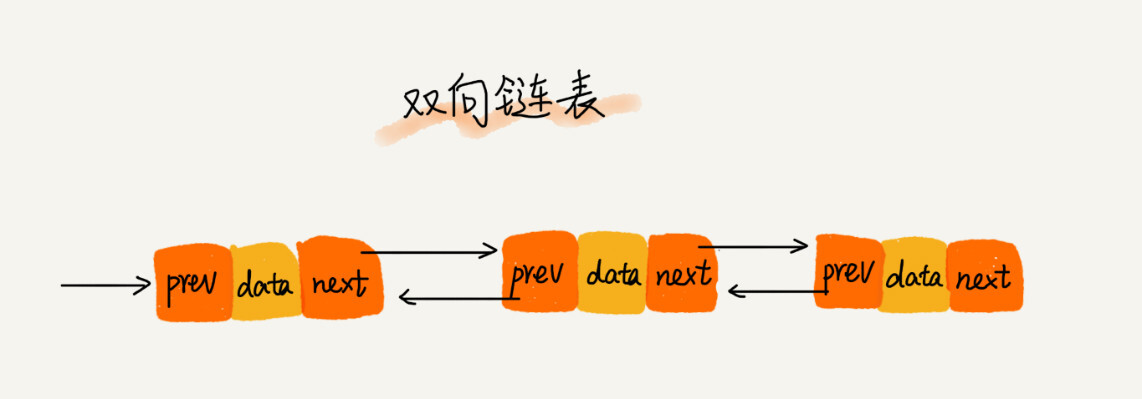
双向链表
双向链表就是在单链表的基础上,给每一个结点加了一个前驱结点这样每个结点不仅能知道后一个结点在哪,前一个结点的位置也知道了。
优点
双向链表可以在时间复杂度为O(1)的情况下找到前一个结点,这样的特点使双向链表在知道结点地址的情况下删除结点等情况下插入、删除操作比单链表更加的高效,如果是单链表的话,是不知道前一个结点的地址的,需要遍历一遍,时间复杂度为O(n),而双向链表为O(1)
空间换时间设计思想
双向链表虽然消耗的内存更多,但是他的性能更好,单链表省内存,但是他的性能低,我们可以根据实际情况选择他们
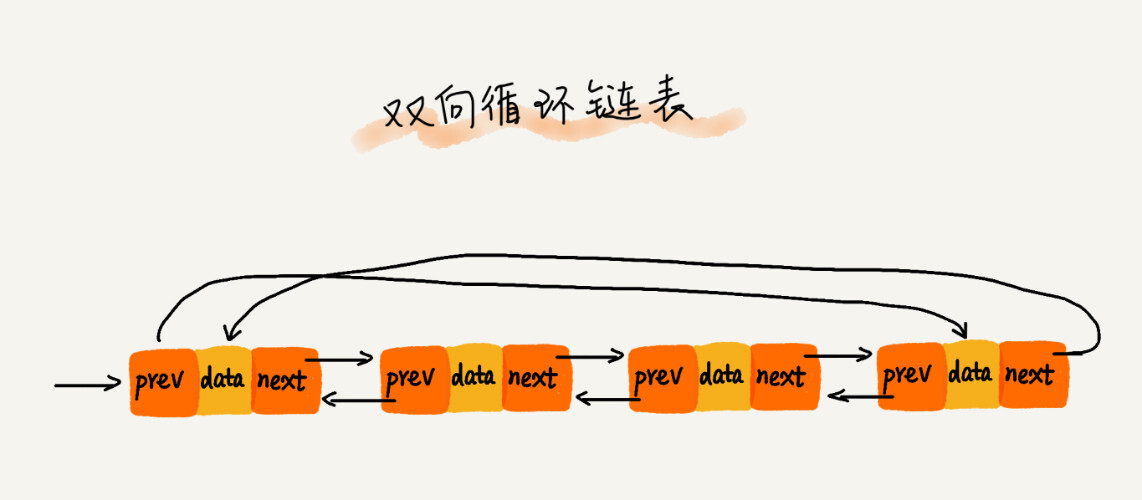
双向循环链表
删除操作的时间复杂度有两种情况
删除结点中“值等于某个给定值”的结点;
删除给定指针指向的结点。
具体情况具体分析
链表实现LRU缓存淘汰策略
常见的三种缓存策略
常见的策略有三种:先进先出策略 FIFO(First In,First out)、最少使用策略LFU(Least Frequently Used)、最近最少使用策略LRU(Least Recently Used)
思路:从链表头插入,如果数据存在,删掉原来的,在重新从头插入,如果数据不存在,在判断缓存是否满了,没满直接从头插入,满了,删除尾结点,在从头插入
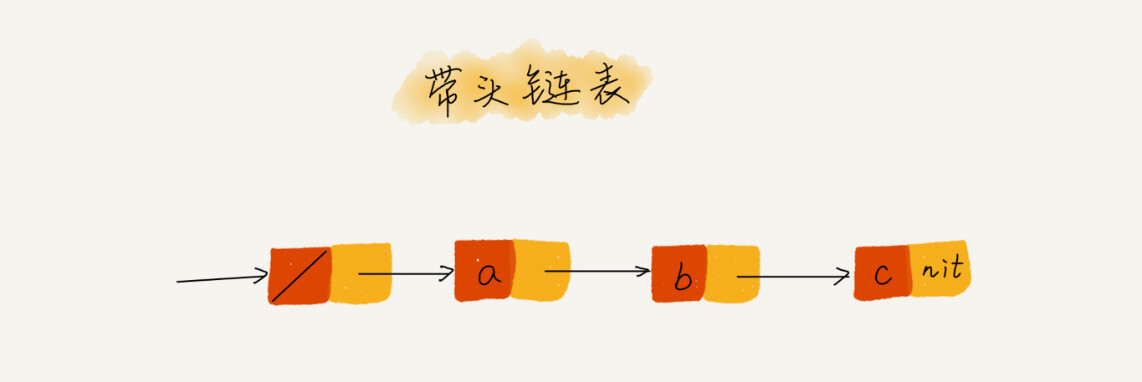
哨兵机制
哨兵是解决编辑问题的,不直接参与业务逻辑
我们知道单链表有头结点和尾结点,如果链表为空,我们插入一个结点的逻辑和正常插入的逻辑是不同的,因为我们不仅要插入结点还要把这个结点作为head,同时删除链表中的结点和尾结点的处理方式也不同
加入一个头结点作为哨兵,不存储数据,尾结点指向头结点,这样的话,面对各种不同的情况,都可以使用同一种处理方式
题目
单链表反转
链表中环检测
两个有序的链表合并
删除链表倒数第n个结点
求链表的中间结点