hdu 1024 MAX Sum Plus Plus【dp】

hdu 1024

题意：给定序列，求找出m个子序列的和使它们最大，子序列无交叉。

题解：又是最大子序列和增强版。但是这回让找m个，我还是没有思路。网上看到的思路无一例外都是：

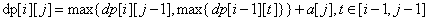
　　dp[i][j]表示前j个数分成i个子序列能获得的最大值。它有两大部分转移过来，一个是j是第i个序列的首元素，则dp[i][j]由dp[i-1][t]转移过来，即前t个数分成i-1个子序列；另一种自然就是第j个数不是第i个子序列的首元素，所以由前j-1个数分成i个子序列的状态dp[i][j-1]转移过来。但是数据很大，二维数组开不下，而且m还未知，所以想优化到一维,dp[j]。用pre[j-1]记录前一个状态，因为当前层状态只由前面一层推过来。不细说了，这里详细解释网上博客一大堆。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 1000000;
const ll INF = 1e12;
int dp[MAXN], pre[MAXN], a[MAXN];

int main()
{
    int n, m, i, j;
    while (scanf("%d%d",&m,&n)==2)
    {
        memset(dp, 0, sizeof(dp));
        memset(pre, 0, sizeof(pre));
        for (i = 1; i <= n; i++)
            scanf("%lld", &a[i]);
        ll MAX;
        for (i = 1; i <= m; i++)
        {
            MAX = -INF;
            for (j = i; j <= n; j++) {
                dp[j] = max(dp[j - 1], pre[j - 1]) + a[j];
                pre[j - 1] = MAX;
                if (MAX < dp[j])
                    MAX = dp[j];
            }
        }
        printf("%lld
", MAX);
    }
    return 0;
}

我看见网上还有人说用滚动数组，一看就是上面的做法，可是我理解的滚动数组是只用一个数组每次求解的时候覆盖和使用上一次的结果。。。。我把dp[]数组改成了二维，第一维大小为2，每次来回换一下就好了。但不知道为啥效率比上面的低好多，不是一样的嘛？再交一回。。。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 1000000;
const ll INF = 1e12;
int dp[2][MAXN], pre[MAXN], a[MAXN];

int main()
{
    int n, m, i, j;
    while (scanf("%d%d",&m,&n)==2)
    {
        memset(dp, 0, sizeof(dp));
        memset(pre, 0, sizeof(pre));
        for (i = 1; i <= n; i++)
            scanf("%lld", &a[i]);
        ll MAX;
        int c=0;
        for (i = 1; i <= m; i++)
        {
            MAX = -INF;
            for (j = i; j <= n; j++) {
                dp[c][j] = max(dp[c][j - 1],dp[c^1][j - 1]) + a[j];
                dp[c ^ 1][j - 1] = MAX;
                if (MAX < dp[c][j])
                    MAX = dp[c][j];
            }
        }
        printf("%lld
", MAX);
    }
    return 0;
}