指令一般都是由两部分组成:操作码和操作地址。
在计算机大量的指令当中有着“二·八”定则,指的是有着20%的指令在80%的时间里重复使用着,而80%的指令只有20%的时间在使用着。
那么为了提高计算机的工作效率,在指令的调用上,要想办法把那20%的指令尽可能的放在近的地方,而那剩下的指令可以放在稍微远一些的地方,因此,赫夫曼编码出现了。
1.赫夫曼编码
赫夫曼(Huffman)编码的基本思想:当各种事件发生的概率不均等时,可对发生概率高的事件用最短的位数(时间)来表示,而对于出现概率比较短的事件,则可以用较长的位数(时间)来表示,从而使总的平均位数(时间)缩短。
下面介绍一下关于赫夫曼编码的方法。
首先要先了解到赫夫曼编码是从下往上的方法构建二叉树。尔其本质就是排序的一种。
当一串数列放在眼前,就需要对其排列,规则为:永远是数列里面两个最小的加在一起后往上走,且两数相加后如遇到等值数列,则放在其右边。在赫夫曼树中永远是小的放在左边而大的放在右边,路径为左零右一。
由一道例题来解释说明
【例题】某台处理机的各条指令使用频度如下表
|
指令 |
使用频度 |
指令 |
使用频度 |
指令 |
使用频度 |
|
ADD |
43% |
JOM |
6% |
CIL |
2% |
|
SUB |
13% |
STO |
5% |
CLA |
22% |
|
JMP |
7% |
SHR |
1% |
STP |
1% |
现在对这个频度表进行赫夫曼编码
先对指令和使用频度进行排序
从小到大为:SHR 1% STP 1% CIL 2% STO 5% JOM 6% JMP 7% SUB 13% CLA 22% ADD 43%
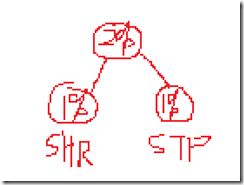
先进行第一次排序,最小的两个先相加
现在的排序是 CIL 2% < 2% < STO 5% < JOM 6% < JMP 7% < SUB 13% < CLA 22% < ADD 43%
加起来的值放在等值的右边
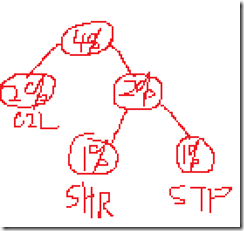
现在的排列是 4% < STO 5% < JOM 6% < JMP 7% < SUB 13% < CLA 22% < ADD 43%
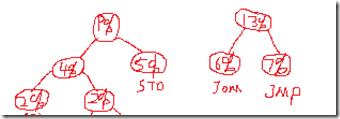
现在的排序是 JOM 6% < JMP 7% < 9% < SUB 13% < CLA 22% < ADD 43%
现在的排序是 9% < SUB 13% < 13% < CLA 22% < ADD 43%
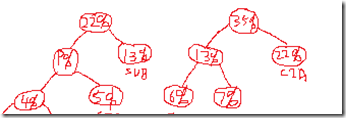
现在的排序是 22% < 35% < ADD 43%
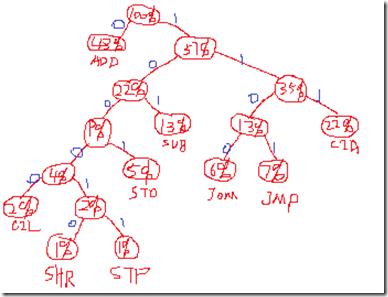
最终的结果为
编码为 SHR 100010 STP 100011 CIL 10000 STO 1001 JOM 1100 JMP 1101 SUB 101 CIA 111 ADD 0
平均码长 = 位长 * 使用频度
2.等长扩展码
在早期的计算机上,为了便于分级译码,一般采用等长扩展码。常见的扩展码有15/15/15或8/64/512。
选用哪种编码方法取决于指令使用频度的分部。若在头15指令中值比较大,但在后30中指令中急剧减少,则应该选择15/15/15;若值的头8种指令中较大,之后64中指令也不太低,则使用8/64/512。
为了方便理解,根据上面那道例题进行练习
由于上面例题编码不长,不用使用15/15/15
我们使用3/3/3和2/7来讨论
3/3/3编码:
频度最高的放在前面:
ADD 00 CIA 01 SUB 10 JMP 11 00 JOM 11 01 STO 11 10 CIL 11 11 00 STP 11 11 01 SHR 11 11 10
2/7编码:
ADD 0 0 CIA 0 1 SUB 1 000 JMP 1 001 JOM 1 010 STO 1 011 CIL 1 100 STP 1 101 SHR 1 110
3.定长扩展码
随着计算机存储空间的日益增大,为保证速度和降低译码复杂度,现很多计算机都采用了固定长度的操作码,所有指令操作码都是同一长度,这就是空间换时间的概念。
以上,不足之处请多多指正。