CF580B Kefa and Company 尺取法

Kefa wants to celebrate his first big salary by going to restaurant. However, he needs company.

Kefa has n friends, each friend will agree to go to the restaurant if Kefa asks. Each friend is characterized by the amount of money he has and the friendship factor in respect to Kefa. The parrot doesn't want any friend to feel poor compared to somebody else in the company (Kefa doesn't count). A friend feels poor if in the company there is someone who has at least d units of money more than he does. Also, Kefa wants the total friendship factor of the members of the company to be maximum. Help him invite an optimal company!

Input

The first line of the input contains two space-separated integers, n and d (1 ≤ n ≤ 10⁵, 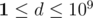) — the number of Kefa's friends and the minimum difference between the amount of money in order to feel poor, respectively.

Next n lines contain the descriptions of Kefa's friends, the (i + 1)-th line contains the description of the i-th friend of type m_i, s_i (0 ≤ m_i, s_i ≤ 10⁹) — the amount of money and the friendship factor, respectively.

Output

Print the maximum total friendship factir that can be reached.

Examples

Input

Copy

4 5
75 5
0 100
150 20
75 1

Output

Copy

100

Input

Copy

5 100
0 7
11 32
99 10
46 8
87 54

Output

Copy

111

Note

In the first sample test the most profitable strategy is to form a company from only the second friend. At all other variants the total degree of friendship will be worse.

In the second sample test we can take all the friends.

双指针扫一遍即可；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 200005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/



ll qpow(ll a, ll b, ll c) {
	ll ans = 1;
	a = a % c;
	while (b) {
		if (b % 2)ans = ans * a%c;
		b /= 2; a = a * a%c;
	}
	return ans;
}

ll n, d;
struct fr {
	ll m, s;
}frd[maxn];

bool cmp(fr x, fr y) {
	return x.m < y.m;
}

ll sum[maxn];

int main()
{
	//ios::sync_with_stdio(0);
	rdllt(n); rdllt(d);
	for (int i = 1; i <= n; i++)rdllt(frd[i].m), rdllt(frd[i].s);
	sort(frd + 1, frd + 1 + n, cmp);
	ll  maxx = -inf;
	int point1 = 1, point2 = 1;
	for (int i = 1; i <= n; i++)sum[i] = sum[i - 1] + frd[i].s;

	while (point2 <= n) {
		if (frd[point2].m - frd[point1].m < d) {
			 maxx = max(maxx, sum[point2] - sum[point1 - 1]);point2++;
		}
		else {
			point1++;

		}
		
	}
	cout << maxx << endl;
    return 0;
}