散列表
散列表:通常,我们称散列的实现为散列表。散列是一种支持常数时间执行插入,删除,查找的技术,但是散列不支持排序操作。因此,FindMax,FindMin诸如此类的操作都将不支持。看到这里,我相信大家都明白我们为什么需要散列表了吧。(它能实现常数时间执行插入,删除,查找的技术)
理想的散列表数据结构是一个包含有关键字的具有固定大小的数组。关键字就是含有某个相关值的字符串(在这里把数字也当做字符串,即:所有的关键字都认为是字符串)
同时把表的大小记作:TableSize。通常让表从0到TableSize - 1变化。
通常是通过散列函数来把关键字映射到0到TableSize - 1这个范围之内的单元之中。理想情况下,散列函数应该运算简单,并且能保证不会在同一个单元出现两个关键字。不过,从实际来看,我们的关键字可能会非常多,而单元的数目有限。所以,我们需要寻找一个合适的散列函数,解决当两个关键字散列到同一个单元的时候(称为冲突),该怎么处理以及如何确定散列表的大小。
散列函数
如果输入的关键字是整数,一般的合理方法就是直接返回mod(key,TableSize)(取余操作)。但是偶尔会遇到关键字的一些不理想的性质。在这种情况下,散列函数的选择就需要慎重了。(比如:表的大小是30,关键字大多数都是30的倍数。这个时候,关键字就会散列到相同的单元去。)较好的办法使得表的大小是个素数,这样散列函数算起来简单而且关键字分配的比较均匀。通常,关键字是字符串。我们可以去这样做,把字符串的每个字符的ASCII值加起来。
既然我们无法保证散列的理想实现(理想情形下,散列应该保证任意两个不同的关键字映射到两个不同的单元),那么无论选择什么样的散列函数都需要解决冲突的发生。其中最简单的两种是分离链接法和开放定址法。
装填因子:散列表中的元素个数与散列表大小的比值定义为装填因子。
开放定址法
所谓开放定址法是指,一旦有冲突发生(该地址单元已经有一个元素了),就去寻找另外的单元,直到找到一个空单元为止。在这种办法中,我们使用的表比较大。更一步的情形是第i次冲突发生,则试探的下一个地址将变化d.由此构造一个散列函数,如式:F(key) = (h(key) + d) mod TableSize;根据d的不同,散列函数从而不同。注意散列的位置不能超过TableSize。一般对于开放定址法而言,装填因子应小于0.5。开放定址法形成的哈希表如下所示,n为数组下标。

线性探测法
将式F(key) = (h(key) + d) mod TableSize中的d选择为i(i表示第几次冲突),就是线性探测法。即:线性探测法以自然序列不断试探散列位置。只要表足够大,总能找到一个位置。但是这样可能会花费很多的时间。其中最坏的情形是,散列函数设计的不行,导致元素占据的位置是聚集在一块的,这样导致每次散列都会试探很多次,才能最终放入。
平方探测法
将式F(key) = (h(key) + d) mod TableSize中的d选择为i²(i表示第几次冲突),就是平方探测法。这是为了解决线性探测法容易出现聚集所提出的。平法探测法随着试探次数的增加,每次跳变寻找的位置将会越来越远。这样就使得元素比较分散。但是有一个糟糕的情形是,一旦表中有一半以上被填满,第一次肯定找不到空单元,并且存在插入失败的可能。(因为最多有表的一半可以用作解决冲突的备选位置)表的大小是素数很重要,因为只有这样才能保证备选位置比较多。
定理:如果使用平法探测,并且表的大小是素数,那么当表中至少有一半是空的时候,总能够插入一个新元素。
在开放定址法中,一般的删除操作是不被支持的,因为相应的单元可能已经引起冲突,元素绕过了它存在了别处,当你将这个位置的元素删除后,那么你后续的查找将会显示找不到该元素,但是你要找的元素确实存在,这就引起了错误。因此在开放定址法中删除一个元素的方式是“懒惰删除”(对该元素做一个标记,表示它被删除)。这样导致的问题是散列表使用的实际空间将会更大。下面给出开放定址法散列实现的ADT。(hashtable.h文件)
#ifndef HASHTABLE_H
#define HASHTABLE_H
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
typedef unsigned int index; //下标
typedef index position;
typedef int ElementType;
typedef struct hash HashTab;
//开放定址法无法真正的删除,只能懒惰删除,因此需要一个标志,使用enum来存放状态
enum MyEnum
{
legitimate, //存在
empty, //空
Remove //移除,这个必须把开头大写一下,因为有个remove函数,否则重定义
};
struct hash
{
ElementType data;
enum MyEnum status; //这个enum变量表示当前空间的状态。
};
typedef struct HashNode
{
int TableSize; //哈希表大小
HashTab *Hash; //哈希表
}* HashTable;
position MyHash(int key, int size); //散列函数
void Insert(ElementType key, HashTable H); //插入
HashTable InitHashTable(int size); //初始化哈希表
void DestroyHashTable(HashTable H); //销毁哈希表
position FindHashTable(ElementType key, HashTable H); //查找
void Delete(ElementType key, HashTable H); //删除
int Prime(int size); //找素数
#endif // !HASHTABLE_H下面是实现上述的ADT操作。
#include "hashtable.h"
position MyHash(int key, int size)
{
position p;
p = key % size; //这个垃圾散列函数将就一下
return p;
}
void Insert(ElementType key, HashTable H)
{
position p;
p = FindHashTable(key, H);
if (H->Hash[p].status != legitimate)
{
//这个p有两种情形,不管哪一种都给data赋值肯定是不会错的
H->Hash[p].data = key;
H->Hash[p].status = legitimate;
}
}
HashTable InitHashTable(int size)
{
HashTable H;
H = (HashTable)malloc(sizeof(struct HashNode));
if (NULL == H)
{
perror("malloc");
}
//为了使得表的尺寸是个素数,寻找size之后的素数。
H->TableSize = Prime(size);
H->Hash = (struct hash *)malloc(sizeof(struct hash)*H->TableSize);
if (NULL == H->Hash)
{
perror("malloc");
}
for (int i = 0; i < H->TableSize; i++)
{
H->Hash[i].status = empty; //初始状态为空
}
return H;
}
void DestroyHashTable(HashTable H)
{
free(H->Hash);
free(H);
H = NULL;
}
position FindHashTable(ElementType key, HashTable H)
{
position p, temp;
int i = 0;
p = MyHash(key, H->TableSize);
temp = p;
//如果不是空,并且不是关键字,接着找。如果是空,说明找不到,或者 H->Hash[p].data == key,说明找到了
while (H->Hash[p].status != empty && H->Hash[p].data != key)
{
i++;
p = temp + i * i; //平方探测
if (p >= H->TableSize)
{
p -= H->TableSize;
}
}
return p; //找到返回该位置,否则返回的是空位置
}
void Delete(ElementType key, HashTable H)
{
position p;
p = FindHashTable(key, H);
if (H->Hash[p].status == empty )
{
printf("哈希表中没有该元素!
");
}
else if (H->Hash[p].status == legitimate)
{
printf("删除成功!
");
H->Hash[p].status = Remove;
}
else
{
printf("该元素已经删除过了,操作无效!
");
}
}
int Prime(int size)
{
//在这里当size足够大的时候可以直接寻找下一个素数
//此处我们为了使得装填因子小于0.5,找到的素数不一定紧挨着size的。
int i, j, temp;
int ret = 0;
size *= 2; //size翻倍
for (i = size + 1;; i += 2)
{
temp = sqrt(i);
for ( j = 2; j <= temp; j++)
{
if (0 == i % j)
{
break;
}
}
if (j > temp)
{
ret = i;
break;
}
}
return ret;
}
测试用的主函数。
#include"hashtable.h"
int main()
{
HashTable H;
H = InitHashTable(10);
//如果size = 10,那么找到的素数是23
Insert(0, H); //边界情形
Insert(3, H);
Insert(12, H);
Insert(33, H);
Insert(91, H);
Insert(67, H);
Insert(5, H);
Insert(28, H);
Insert(48, H);
Insert(23, H); //边界情形
position p;
p = FindHashTable(23, H);
if (legitimate == H->Hash[p].status)
{
printf("找到了,在位置%d处
",p);
}
else
{
printf("未找到该元素!
");
}
p = FindHashTable(0, H);
if (legitimate == H->Hash[p].status)
{
printf("找到了,在位置%d处
", p);
}
else
{
printf("未找到该元素!
");
}
p = FindHashTable(14, H);
if (legitimate == H->Hash[p].status)
{
printf("找到了,在位置%d处
", p);
}
else
{
printf("未找到该元素!
");
}
Delete(3, H);
Delete(3, H);
DestroyHashTable(H);
system("pause");
return 0;
}测试结果如下:
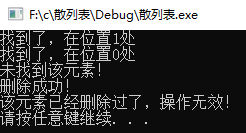
散列表的基本操作就这么多。但是平法探测法仍旧会引起聚集,但是好的是一般还能接受。平方探测法如果元素填的太满(装填因子很大),那么操作将会花费很长的时间,并且Insert操作可能会失败。这时一种解决办法是建立一个新的表,这个表示现在哈希表的两倍大(并且使用一个新的散列函数)。扫描旧的散列表中元素,并且重新散列到新的散列表中。这个操作称之为再散列(rehashing)。显然这个操作的代价非常高。运行时间O(N)。表的大小2N。好的一点是,再散列不会经常发生。当然,到底什么时候再散列这是一个很重要的问题。再散列的实现比较简单。
HashTable Rehash(HashTable H)
{
int oldsize = H->TableSize;
struct hash * oldhash = H->Hash;
H = InitHashTable(2 * oldsize);
for (int i = 0; i < oldsize; i++)
{
if (oldhash[i].status == legitimate)
{
Insert(oldhash[i].data, H);
}
}
free(oldhash);
return H;
}分离链接法
分离链接法可以避开表过大这个缺点。但是它需要使用指针给新单元分配内存,这样也会造成比较大的开销。因此算法的速度就降下来了。使用该方法的时候要求表应该尽量的短,这样才能在常数时间内完成插入,删除,查找操作。分离链接法在使用的时候,一般装填因子都会接近1。分离链接法形成的表如下所示。蓝色方块表示链表。
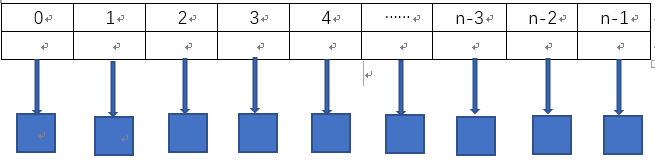
分离链接法实现哈希表的代码如下。
ADT(hashmap.h文件)
#ifndef HASHMAP_H
#define HASHMAP_H
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
typedef int ElementType;
typedef struct ListNode //链表节点
{
ElementType data;
struct ListNode * next;
}* List;
typedef List Position;
typedef struct HashNode //哈希表
{
int TableSize;
List Hash;
}* HashMap;
HashMap InitHashMap(int size);
void InsertHashMap(ElementType key, HashMap H);
Position FindHashMap(ElementType key, HashMap H);
void DeleteHashMap(ElementType key, HashMap H);
int HashFuction(ElementType key,int size);
int NextPrime(int size);
#endif // !HASHMAP_H操作集实现代码(hashmap.c文件)
#include "hashmap.h"
HashMap InitHashMap(int size)
{
HashMap H;
H = (HashMap)malloc(sizeof(struct HashNode));
if (NULL == H)
{
perror("malloc");
}
H->TableSize = NextPrime(size);
H->Hash = (List)malloc(sizeof(struct ListNode)*H->TableSize);
if (NULL == H)
{
perror("malloc");
}
for (int i = 0; i < H->TableSize; i++)
{
H->Hash[i].next = NULL;
}
return H;
}
void InsertHashMap(ElementType key, HashMap H)
{
Position p = FindHashMap(key, H);
List node;
int index = HashFuction(key, H->TableSize);
if (NULL == p)
{
node = (List)malloc(sizeof(struct ListNode));
node->data = key;
node->next = H->Hash[index].next;
H->Hash[index].next = node;
}
else
{
; //已存在就什么都不干
}
}
Position FindHashMap(ElementType key, HashMap H)
{
Position p;
List l;
int index = HashFuction(key, H->TableSize);
l = H->Hash[index].next;
p = l;
while(NULL != p && p->data != key)
{
p = p->next;
}
return p;
}
void DeleteHashMap(ElementType key, HashMap H)
{
Position p = FindHashMap(key, H);
List temp;
int index = HashFuction(key, H->TableSize);
if (NULL == p)
{
printf("该元素不存在!
");
}
else
{
temp = &H->Hash[index];
while (temp->next != p)
{
temp = temp->next;
}
temp->next = temp->next->next;
free(p);
printf("删除成功!
");
}
}
int HashFuction(ElementType key, int size)
{
int index;
index = key % size;
return index;
}
int NextPrime(int size)
{
int ret;
for (int i = size + 1; ; i++)
{
for (int j = 2; j <= sqrt(i); j++)
{
if (0 == i%j)
{
break;
}
}
ret = i;
break;
}
return ret;
}测试代码(main.c)
#include"hashmap.h"
int main()
{
HashMap H;
H = InitHashMap(10);
InsertHashMap(4, H);
InsertHashMap(23, H);
InsertHashMap(45, H);
InsertHashMap(13, H);
InsertHashMap(45, H);
InsertHashMap(48, H);
InsertHashMap(54, H);
InsertHashMap(43, H);
InsertHashMap(19, H);
InsertHashMap(74, H);
InsertHashMap(83, H);
InsertHashMap(75, H);
InsertHashMap(90, H);
InsertHashMap(63, H);
InsertHashMap(65, H);
InsertHashMap(93, H);
if (NULL != FindHashMap(3,H))
{
printf("找到了!
");
}
else
{
printf("没有该元素!
");
}
if (NULL != FindHashMap(23, H))
{
printf("找到了!
");
}
else
{
printf("没有该元素!
");
}
if (NULL != FindHashMap(93, H))
{
printf("找到了!
");
}
else
{
printf("没有该元素!
");
}
if (NULL != FindHashMap(73, H))
{
printf("找到了!
");
}
else
{
printf("没有该元素!
");
}
DeleteHashMap(4, H);
if (NULL != FindHashMap(4, H))
{
printf("找到了!
");
}
else
{
printf("没有该元素!
");
}
system("pause");
return 0;
}测试结果如下:

散列表的应用
在编译器设计方面,编译器使用散列表跟踪源代码中声明的变量。这种数据叫做符号表。
散列表还可以用于在线拼写检查。假设将整个词典先散列,单次可以在常数时间内被检测。散列表就表现的很好。
总结
散列表是一种能在常数时间内实现insert和find操作的数据结构。在某些快速查找的场合,散列是一个非常好的选择。但是它不支持任何排序操作。另外对于散列表来说,有两点非常重要。
- 装填因子不能过大,在装填因子大于0.85的时候,散列表现的很糟糕,并且对于开放定址法而言,insert操作可能失败。一般我们都让装填因子保持在0.5以下。
- 影响散列表性能的另一个关键因素是散列函数的选择,一个好的散列函数能起到事半功倍的效果。