BZOJ 2595: [Wc2008]游览计划（斯坦纳树）

http://www.lydsy.com/JudgeOnline/problem.php?id=2595

题意：

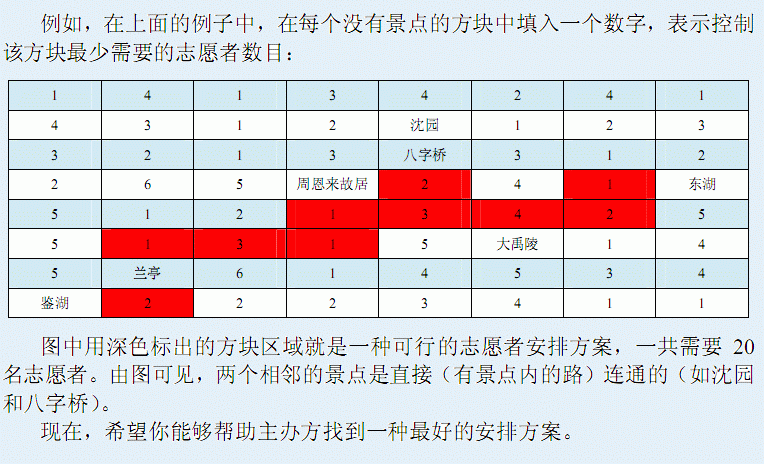
思路：

学习了一下斯坦纳树，这个我老是想到lol中的斯卡纳。。。

斯坦纳树和最小生成树是差不多的，斯坦纳树是将给定点连接起来的最小代价，可以额外增加点。主要是通过状压dp和spfa来做。

f [ i ] [ j ] [ now ] 表示以$(i,j)$为根节点并且状态为now时的最小代价。

它有两个状态转移方程：

f[i][j][now]=min(f[i][j][now],f[i][j][s]+f[i][j][now-s]-a[i][j]) 

这个是枚举子集，将两颗子树合并起来，要注意的一点就是根节点a[i][j]会重复计算依次，这也就是为什么最后还要减去a[i][j]。

至于枚举子集的方法就是：

for(int sub=(state-1)&state;sub;sub=(sub-1)&state)

另一个状态转移方程就是：

f[i][j][now]=min(f[i][j][now],f[i'][j'][now]+a[i][j])

这个就是往上下左右四个方向拓展，因为当一个状态的最优解确定，与它相邻的节点的最优解也就能确定下来。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<sstream>
#include<vector>
#include<stack>
#include<queue>
#include<cmath>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef pair<int,ll> pll;
const int INF = 0x3f3f3f3f;
const int maxn=100+5;

int n, m, k;
int a[15][15];
int ans[15][15];
int inq[20005];
int f[15][15][2005];

int dx[5]={1,-1,0,0};
int dy[5]={0,0,1,-1};

struct node
{
    int i,j,state;
}path[15][15][2005];

struct point
{
    int i,j;
};

queue<point> Q;

int c(point x)
{
    return (x.i-1)*n+x.j;
}

void spfa(int state)
{
    while (!Q.empty())
    {
        point x=Q.front(); Q.pop(); inq[c(x)]=0;
        for (int k=0;k<4;k++)
        {
            point y;
            y.i=x.i+dx[k],y.j=x.j+dy[k];
            if (y.i<1||y.j<1||y.i>n||y.j>m) continue;
            if (f[y.i][y.j][state]>f[x.i][x.j][state]+a[y.i][y.j])
            {
                f[y.i][y.j][state]=f[x.i][x.j][state]+a[y.i][y.j];
                path[y.i][y.j][state].i=x.i,path[y.i][y.j][state].j=x.j,path[y.i][y.j][state].state=state;
                if (!inq[c(y)])  {Q.push(y),inq[c(y)]=1;}
            }
        }
    }
}

void dfs(int x, int y, int state)
{
    if(!path[x][y][state].state)  return;
    ans[x][y]=1;
    dfs(path[x][y][state].i,path[x][y][state].j,path[x][y][state].state);
    if(path[x][y][state].i==x && path[x][y][state].j==y)
        dfs(x,y,state^path[x][y][state].state);
}

int main()
{
    //freopen("in.txt","r",stdin);
    while(~scanf("%d%d",&n,&m))
    {
        k=0;
        memset(f,0x3f,sizeof(f));
        memset(ans,0,sizeof(ans));
        memset(path,0,sizeof(path));
        for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
            if(!a[i][j])  f[i][j][1<<(k++)]=0;
        }

        for(int state=1;state<(1<<k);state++)
        {
            for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
            {
                for(int sub=(state-1)&state;sub;sub=(sub-1)&state)   //枚举子集,将两个子树合并
                {
                    if(f[i][j][state]>f[i][j][sub]+f[i][j][state-sub]-a[i][j])  //将两颗树合并，a[i][j]这个根顶点会多算一次，减掉
                    {
                        f[i][j][state]=f[i][j][sub]+f[i][j][state-sub]-a[i][j];
                        path[i][j][state].i=i,path[i][j][state].j=j,path[i][j][state].state=sub; //路径记录
                    }
                }
                if(f[i][j][state]!=INF)
                {
                    point p;
                    p.i=i, p.j=j;
                    Q.push(p); inq[c(p)]=1;
                }
            }
            spfa(state);
        }

        int x,y;
        for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(!a[i][j])  {x=i;y=j;break;}

        printf("%d
",f[x][y][(1<<k)-1]);

        dfs(x,y,(1<<k)-1);
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(!a[i][j])  printf("x");
                else if(ans[i][j])  printf("o");
                else printf("_");
            }
            printf("
");
        }
    }
    return 0;
}