http://poj.org/problem?id=3281
Description
Cows are such finicky eaters. Each cow has a preference for certain foods and drinks, and she will consume no others.
Farmer John has cooked fabulous meals for his cows, but he forgot to check his menu against their preferences. Although he might not be able to stuff everybody, he wants to give a complete meal of both food and drink to as many cows as possible.
Farmer John has cooked F (1 ≤ F ≤ 100) types of foods and prepared D (1 ≤ D ≤ 100) types of drinks. Each of his N (1 ≤ N ≤ 100) cows has decided whether she is willing to eat a particular food or drink a particular drink. Farmer John must assign a food type and a drink type to each cow to maximize the number of cows who get both.
Each dish or drink can only be consumed by one cow (i.e., once food type 2 is assigned to a cow, no other cow can be assigned food type 2).
Input
Line 1: Three space-separated integers: N, F, and D
Lines 2..N+1: Each line i starts with a two integers Fi and Di, the number of dishes that cow i likes and the number of drinks that cow i likes. The next Fi integers denote the dishes that cow i will eat, and the Di integers following that denote the drinks that cow i will drink.
Output
Line 1: A single integer that is the maximum number of cows that can be fed both food and drink that conform to their wishes
Sample Input
4 3 3 2 2 1 2 3 1 2 2 2 3 1 2 2 2 1 3 1 2 2 1 1 3 3
Sample Output
3
Hint
One way to satisfy three cows is:
Cow 1: no meal
Cow 2: Food #2, Drink #2
Cow 3: Food #1, Drink #1
Cow 4: Food #3, Drink #3
The pigeon-hole principle tells us we can do no better since there are only three kinds of food or drink. Other test data sets are more challenging, of course.
题意分析:
有n头牛,每头牛有爱吃的食物和水,每个食物和水只有一个,求最多有多少牛可以同时吃到爱吃的食物和饮料。
解题思路:
将食物和牛之间建边,牛和牛建边,牛和水建边,水和汇点建边,求最大流。
注意牛和牛建边:
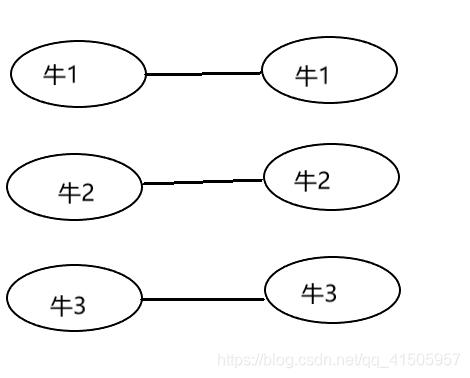
保证了每只牛通过的流量为1,因为1头牛不能多次算。
#include <stdio.h>
#include <algorithm>
#include <queue>
#include <string.h>
#define N 550
using namespace std;
int n, f, d, inf=0x7f7f7f;
int e[N][N], flow[N], pre[N];
int bfs(int s, int t)
{
int u, v;
queue<int>q;
q.push(s);
flow[s] = inf;
while (!q.empty())
{
u = q.front();
q.pop();
if (u == t)
break;
for (v = 1; v <= 2*n + f + d + 1; v++)
{
if (e[u][v] && pre[v] == -1 && v != s)
{
pre[v] = u;
q.push(v);
flow[v] = min(flow[u], e[u][v]);
}
}
}
if (pre[t] == -1)
return -1;
return flow[t];
}
int EK(int s, int t)
{
int num, sum = 0, p;
while (1)
{
memset(pre, -1, sizeof(pre));
num = bfs(s, t);
if (num == -1)
return sum;
sum += num;
p = t;
while (p != s)
{
e[pre[p]][p] -= num;
e[p][pre[p]] += num;
p = pre[p];
}
}
return sum;
}
int main()
{
int fi, di, i, u;
while (scanf("%d%d%d", &n, &f, &d) != EOF)
{
memset(e, 0, sizeof(e));
for (i = 1; i <= f; i++)
e[0][i] = 1;
for (i = 1; i <= d; i++)
e[f + 2*n + i][f + 2*n + d + 1] = 1;
for (i = 1; i <= n; i++)
{
e[i+f][i+n+f]=1;
scanf("%d%d", &fi, &di);
while (fi--) {
scanf("%d", &u);
e[u][i + f] = 1;
}
while (di--) {
scanf("%d", &u);
e[i + f + n][u + 2*n + f] = 1;
}
}
printf("%d
", EK(0, f + 2*n + d + 1));
}
return 0;
}