误差反向传播法
前言
此为本人学习《深度学习入门》的学习笔记
四、简单层的实现
本节将用 Python 实现前面的购买苹果的例子。这里,我们把要实现的计算图的乘法节点称为“乘法层”(MulLayer),加法节点称为“加法层”(AddLayer)。
1、乘法层的实现
层的实现中有两个共通的方法(接口)forward() 和backward()。forward() 对应正向传播,backward() 对应反向传播。
实现乘法层。乘法层作为 MulLayer 类,其实现过程如下所示
class MulLayer: def __init__(self): self.x = None self.y = None def forward(self, x, y): self.x = x self.y = y out = x * y return out def backward(self, dout): dx = dout * self.y # 翻转x和y dy = dout * self.x return dx, dy
__init__() 中会初始化实例变量 x 和 y,它们用于保存正向传播时的输入值。forward() 接收 x 和 y 两个参数,将它们相乘后输出。backward() 将从上游传来的导数(dout)乘以正向传播的翻转值,然后传给下游。
使用 MulLayer 实现前面的购买苹果的例子(2 个苹果和消费税)。
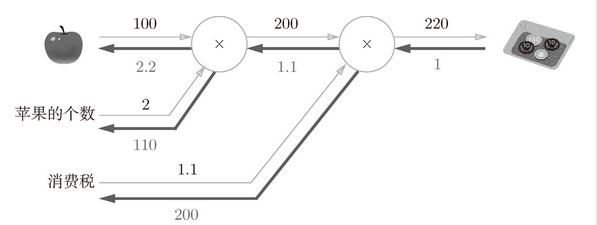
图 5-16 购买 2 个苹果
使用这个乘法层的话,图 5-16 的正向传播可以像下面这样实现

此外,关于各个变量的导数可由 backward() 求出。

调用 backward() 的顺序与调用 forward() 的顺序相反。此外,要注意 backward() 的参数中需要输入“关于正向传播时的输出变量的导数”。比如,mul_apple_layer 乘法层在正向传播时会输出 apple_price,在反向传播时,则会将 apple_price 的导数 dapple_price 设为参数。
2、加法层的实现
class AddLayer: def __init__(self): pass def forward(self, x, y): out = x + y return out def backward(self, dout): dx = dout * 1 dy = dout * 1 return dx, dy
加法层不需要特意进行初始化,所以 __init__() 中什么也不运行(pass 语句表示“什么也不运行”)。加法层的 forward() 接收 x 和 y 两个参数,将它们相加后输出。backward() 将上游传来的导数(dout)原封不动地传递给下游。
使用加法层和乘法层,实现图 5-17 所示的购买 2 个苹果和 3 个橘子的例子。
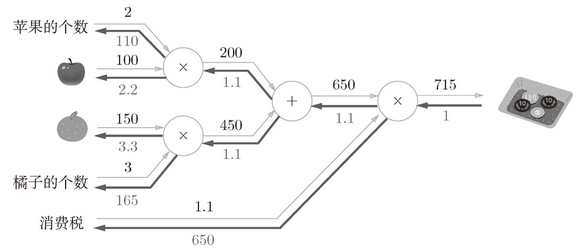
图 5-17 购买 2 个苹果和 3 个橘子
用 Python 实现图 5-17 的计算图的过程如下所示

首先,生成必要的层,以合适的顺序调用正向传播的 forward() 方法。然后,用与正向传播相反的顺序调用反向传播的 backward() 方法,就可以求出想要的导数。
五、激活函数层的实现
将计算图的思路应用到神经网络中。把构成神经网络的层实现为一个类。先来实现激活函数的 ReLU 层和 Sigmoid 层。
1、ReLU层
激活函数 ReLU(Rectified Linear Unit)由下式(5.7)表示。

通过式(5.7),可以求出 y 关于 x 的导数,如式(5.8)所示。

在式(5.8)中,如果正向传播时的输入 x 大于 0,则反向传播会将上游的值原封不动地传给下游。反过来,如果正向传播时的 x 小于等于 0,则反向传播中传给下游的信号将停在此处。用计算图表示的话,如图 5-18 所示。
实现 ReLU 层。在神经网络的层的实现中,一般假定 forward() 和backward() 的参数是 NumPy 数组。

图 5-18 ReLU 层的计算图
class Relu: def __init__(self): self.mask = None def forward(self, x): self.mask = (x <= 0) out = x.copy() out[self.mask] = 0 return out def backward(self, dout): dout[self.mask] = 0 dx = dout return dx
Relu 类有实例变量 mask。这个变量 mask 是由 True/False 构成的 NumPy 数组,它会把正向传播时的输入 x 的元素中小于等于 0 的地方保存为 True,其他地方(大于 0 的元素)保存为 False。

2、Sigmoid层
实现sigmoid函数,sigmoid函数由式(5.9)表示
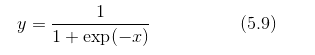
用计算图表示式子(5.9)的话,则如图5-19所示
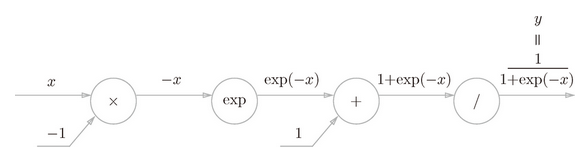
图 5-19 sigmoid 层的计算图(仅正向传播)
图 5-19 中,除了“×”和“+”节点外,还出现了新的“exp”和“/”节点。“exp”节点会进行 y = exp(x) 的计算,“/”节点会进行 的计算。
如图 5-19 所示,式(5.9)的计算由局部计算的传播构成。
下面我们就来进行图 5-19 的计算图的反向传播。这里,作为总结,我们来依次看一下反向传播的流程。
步骤 1
“/”节点表示 ,它的导数可以解析性地表示为下式。
根据式(5.10),反向传播时,会将上游的值乘以 (正向传播的输出的平方乘以 -1 后的值)后,再传给下游。计算图如下所示。

步骤 2
“+”节点将上游的值原封不动地传给下游。计算图如下所示。

步骤 3
“exp”节点表示 y = exp(x),它的导数由下式表示。
计算图中,上游的值乘以正向传播时的输出(这个例子中是 exp(-x))后,再传给下游。

步骤 4
“×”节点将正向传播时的值翻转后做乘法运算。因此,这里要乘以 -1。

图 5-20 Sigmoid 层的计算图
