算法初探

更新记录

【1】2020.07.21-11:40

• 1.完善A*内容

正文

[A problem]

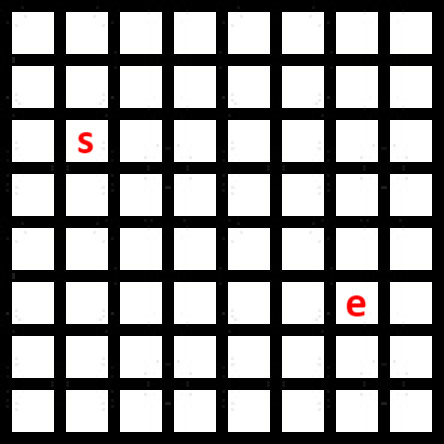
如果让你在这么一个方格图中寻找最短路径，你会怎么做？

Student-A：我会广度优先算法！
Student-B[最优]：我会贪心走过去！

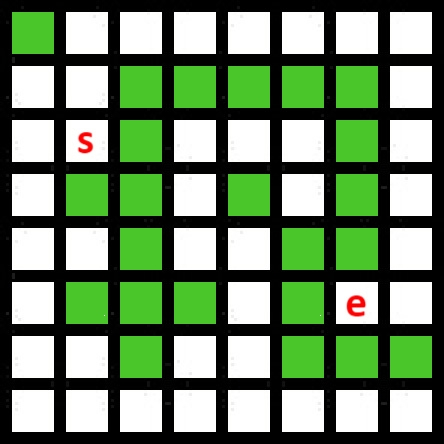
上面是最简单的状况，如果有障碍物呢？
注：绿色格子不可通过

Student-A：我会广度优先算法与深度优先算法！
Student-B：我。。

看起来此问题得到了解决，但是我们可以很快想到：朴素的搜索算法最坏情况下竟需要遍历整个图！！

那么我们此时需要剪枝，那么如何剪呢？
最容易想到的就是在某一步发现不管怎么样，都不可能达到目标情况或不是最优解，此时直接回溯，效率提高不少

用一个式子来表示就是：

(s+h(s)>dep)

(s)就是当前的步数，(dep)就是目标
那么其中的(h(s))就是对当前的一个估计，称为估价函数

当前步数+估计>目标，你还会走下去吗？

当然不会，所以直接回溯

容易发现，估价函数越准确，(s)越小，程序越快；估计函数越不准，(s)越大，程序越慢

在寻找最短路的问题中，(h(s))就是代表当前到终点的距离

在不同的问题中，(h(s))也有不同的含义

P1379 八数码难题

这里的(h(s))就是没有在正确位置上的数的个数

首先计算(dep)，即最少几步即可到达目标状况
随着广度的放宽，慢慢进行A*搜索寻找答案

函数中

if(!dis) return 1;
if(s+dis>stdep) return 0;

就是A*的核心

#include<iostream>
#include<cstdio>
#define R register
int goalx[9]={0,1,2,3,3,3,2,1,1},movx[4]={1,-1,0,0},zx;
int goaly[9]={0,1,1,1,2,3,3,3,2},movy[4]={0,0,1,-1},zy;
int stdep;
std::string begin;
inline int abs(int a){return a<0?-a:a;}
inline int GetRow(int a){return a%3+1;}
inline int GetColumn(int a){return a/3+1;}
inline int GetOriginal(int x,int y){return x-1+(y-1)*3;}
inline int GetDist(std::string a){
	int dist=0,now=0;
	for(R int i=0;i<a.length();i++){
		now=a[i]-'0';
		if(!now){
			zx=GetRow(i),zy=GetColumn(i);
			continue;
		}
		dist+=(abs(GetRow(i)-goalx[now]) + abs(GetColumn(i)-goaly[now]));
	}
	return dist;
}
inline bool A_star(int s,int pre){
	int dis=GetDist(begin);
	if(!dis) return 1;
	if(s+dis>stdep) return 0;
	for(R int i=0;i<4;i++){
		int past=GetOriginal(zx,zy);
		zx+=movx[i],zy+=movy[i];
		int now=GetOriginal(zx,zy);
		if(zx<1||zy<1||zx>3||zy>3||now==pre){
			zx-=movx[i],zy-=movy[i];continue;
		}
		std::swap(begin[past],begin[now]);
		if(A_star(s+1,past))
			return 1;
		std::swap(begin[past],begin[now]);
		zx-=movx[i],zy-=movy[i];
	}
	return 0;
}
signed main(){
	std::ios::sync_with_stdio(0);
	std::cin>>begin;
	stdep=GetDist(begin);
	while(stdep<30){
		if(A_star(0,-1))
			break;
		stdep+=1;
	}
	std::cout<<stdep;
}

P2324 [SCOI2005]骑士精神

同上，这里的(h(s))是没有在正确位置上的棋子的个数

#include<iostream>
#include<cstdio>
#define R register
using std::string;
string goal[5]={"11111","01111","00*11","00001","00000"},in[5];
int mx[8]={1,1,-1,-1,2,2,-2,-2},sx;
int my[8]={2,-2,2,-2,1,-1,1,-1},sy;
int t,dep;
inline int GetDist(string a[5]){
	int dist=0;
	for(R int i=0;i<5;i++)
		for(R int o=0;o<5;o++){
			if(a[i][o]=='*'){
				sx=i,sy=o;
				continue;
			}
			if(a[i][o]!=goal[i][o]) dist+=1;
		}
	return dist;
}
inline bool A_star(int s,int prex,int prey){
	int dis=GetDist(in);
	if(!dis) return 1;
	if(s+dis>dep) return 0;
	int sx2=sx,sx3=sx,sy2=sy,sy3=sy;
	for(R int i=0;i<8;i++){
		sx2+=mx[i],sy2+=my[i];
		if(sx2<0||sy2<0||sx2>4||sy2>4||(prex==sx2&&prey==sy2)){
			sx2-=mx[i],sy2-=my[i];
			continue;
		}
		std::swap(in[sx3][sy3],in[sx2][sy2]);
		if(A_star(s+1,sx3,sy3)) return 1;
		std::swap(in[sx3][sy3],in[sx2][sy2]);
		sx2-=mx[i],sy2-=my[i];
	}
	return 0;
}
signed main(){
	scanf("%d",&t);
	while(t--){
		for(int i=0;i<5;i++) std::cin>>in[i];
		dep=GetDist(in);
		while(dep<16){
			if(A_star(0,-1,-1))
				break;
			dep+=1;
		}
		if(dep==16) printf("-1
");
		else printf("%d
",dep);
	}
}

UVA1343 旋转游戏 The Rotation Game

这里的(h(s))是八宫格内还缺几个数就满足题意

读入比较恶心，要小心写代码

我这篇好像是Luogu最优解

#include<iostream>
using std::cin;
using std::cout;
char f[5][8],lu[100],Map[8]={'A','B','C','D','E','F','G','H'};
int shrc[8]={1,2,3,4,2,1,4,3},dep;
int shru[8]={0,0,1,1,1,1,0,0},ans;
inline int Tmax(int a,int b,int c){return a>b?(a>c?a:c):(b>c?b:c);}
inline int GetSituation(){
	int a[4]={0,0,0,0};
	a[f[1][3]-'0']+=1;a[f[1][4]-'0']+=1;a[f[1][5]-'0']+=1;
	a[f[2][3]-'0']+=1;a[f[2][4]-'0']+=1;a[f[2][5]-'0']+=1;
	a[f[3][4]-'0']+=1;a[f[4][4]-'0']+=1;
	return 8-Tmax(a[1],a[2],a[3]);
}
inline void Change(char a[8],int rc,bool rule){
	char head;
	if(rule){
		head=a[7];
		for(int i=6;i>0;i--) a[i+1]=a[i];
		a[1]=head; 
	}
	else{
		head=a[1];
		for(int i=1;i<7;i++) a[i]=a[i+1];
		a[7]=head;
	}
	switch(rc){
		case 1: f[3][3]=f[1][3],f[4][3]=f[1][5];break;
		case 2: f[3][5]=f[2][3],f[4][5]=f[2][5];break;
		case 3: f[1][3]=f[3][3],f[2][3]=f[3][5];break;
		case 4: f[1][5]=f[4][3],f[2][5]=f[4][5];break;
	}
}
inline bool A_star(int s,int prc,int pru){
	int st=GetSituation();
	if(!st){
		ans=f[1][3]-'0';
		return 1;
	}
	if(s+st>dep) return 0;
	for(int i=0;i<8;i++){
		if(shrc[i]==prc&&shru[i]!=pru) continue;
		Change(f[shrc[i]],shrc[i],shru[i]);
		lu[s]=Map[i];
		if(A_star(s+1,shrc[i],shru[i])) return 1;
		Change(f[shrc[i]],shrc[i],!shru[i]);
	}
	return 0;
}
signed main(){
	while(1){
		cin>>f[1][1];if(f[1][1]=='0') break;
		cin>>f[2][1]>>f[1][2]>>f[2][2];
		for(int i=1;i<8;i++) cin>>f[3][i];
		f[1][3]=f[3][3],f[2][3]=f[3][5];
		cin>>f[1][4]>>f[2][4];
		for(int i=1;i<8;i++) cin>>f[4][i];
		f[1][5]=f[4][3],f[2][5]=f[4][5];
		cin>>f[1][6]>>f[2][6]>>f[1][7]>>f[2][7];
		dep=GetSituation();ans=f[1][3]-'0';
		while(!A_star(0,-1,-1)) dep+=1;
		if(!dep) cout<<"No moves needed";
		else for(int i=0;i<dep;i++) cout<<lu[i];
		cout<<"
"<<ans<<"
";
	}
}

容易发现，A*与IDA*就是在原搜索的基础上加上几行优化的东西，所以启发式搜索并没有那么难