圆方树

圆方树相关知识

我们在做题的时候会发现：很多时候树比图好维护的多

例如求两点间路径长度，链上加法等

而在一些题中，应用圆方树能将图化为一棵树

---

圆方树最初用来处理仙人掌图，但是我们很多时候也能在一般无向图上使用

首先抛一个很大众的名词：点双连通图

点双连通图就是一个任意两点间都有至少两条除起点终点外，中间点不重复的路径的图

用兔队的话说一个近乎等价的定义就是不存在割点的图

为啥说是近乎等价呢？因为这个图：

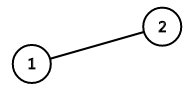
它没有割点，但是不是点双联通

然后是另一个名词：点双联通分量

点双联通分量就是一个极大的点双联通子图

一个点可能属于多个点双，但是一条边恰好属于一个，或是不属于任何一个点双

我们把每个点双缩成一个方点，然后原来的点双上的点向方点连边

我们会发现原来的割点就是点双分割点，每个点双形成了一个星图

圆方树的构建

我们利用tarjan算法构建圆方树

fx(void,tarjan)(int now){
	low[now]=dfn[now]=++dfsc;
	stk[++top]=now;
//tarjan基本操作
	ann+=1;
//统计一个联通图中的点的个数
	for(R int i=head[now];i;i=e[i].na){
		if(!dfn[e[i].np]){
//是否访问过
			tarjan(e[i].np);
			low[now]=min(low[now],low[e[i].np]);
//追溯
			if(low[e[i].np]==dfn[now]){
				cnt+=1;
//方点+1
				do{
					add(sqh,sqe,snum,cnt,stk[top]);
					add(sqh,sqe,snum,stk[top],cnt);
					sqrn[cnt]+=1;
				} while(stk[top--]!=e[i].np);
				add(sqh,sqe,snum,cnt,now);
				add(sqh,sqe,snum,now,cnt);
//点双上的点向方点连边
			}
		} else low[now]=min(low[now],dfn[e[i].np]);
//访问过，更新
	}
}

圆方树例题

P4630 [APIO2018] Duathlon 铁人两项

题目链接

求互不相同的三元组 (langle s,c,f angle) 的个数，其中 (langle s,c,f angle) 表示存在一条简单路径 (s o f)，这条路径经过 (c)

有个显然的性质：给定一个点双中的点 (a)，点双中的另外两个点 (b,c) 之间一定存在一条简单路径经过 (a)

那么所有路径并起来，就恰好完全等于这个点双

设方点集合为 (S)，路径集合为 (R)，设 (sin S,rin R) 那么 (sin r) 当且仅当这条路径经过 (s)

本题就是求：

[sumlimits_{sin S}sumlimits_{rin s}1 ]

设一个方点上面有 (n) 个子树，下面有 (m) 个子树，此方点做出的贡献就是

[sumlimits_{i=1}^nsumlimits_{j=1}^m ext{size}_i imes ext{size}_j ]

利用乘法结合律即可 (O(n)) 求出

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 1000001
#define M 5001
#define INF 1100000000
#define Kafuu return
#define Chino 0
#define fx(l,n) inline l n
#define set(l,n,ty,len) memset(l,n,sizeof(ty)*len)
#define cpy(f,t,ty,len) memcpy(t,f,sizeof(ty)*len)
#define int long long
#define R register
#define C const
using namespace std;
int n,m,fr,to,head[N],sqh[N],num,snum,sqrn[N],cnt,dfsc,dfn[N],low[N],ann,top,stk[N],size[N],ans;
struct Edge{
	int na,np;
}e[N],sqe[N];
fx(void,add)(int *head,Edge *e,int &num,int f,int t){
	e[++num].na=head[f];
	e[num].np=t;
	head[f]=num;
}
fx(int,gi)(){
	R char c=getchar();R int s=0,f=1;
	while(c>'9'||c<'0'){
		if(c=='-') f=-f;
		c=getchar();
	}
	while(c<='9'&&c>='0') s=(s<<3)+(s<<1)+(c-'0'),c=getchar();
	return s*f;
}
fx(void,tarjan)(int now){
	low[now]=dfn[now]=++dfsc;
	stk[++top]=now;
	ann+=1;
	for(R int i=head[now];i;i=e[i].na){
		if(!dfn[e[i].np]){
			tarjan(e[i].np);
			low[now]=min(low[now],low[e[i].np]);
			if(low[e[i].np]==dfn[now]){
				cnt+=1;
				do{
					add(sqh,sqe,snum,cnt,stk[top]);
					add(sqh,sqe,snum,stk[top],cnt);
					sqrn[cnt]+=1;
				} while(stk[top--]!=e[i].np);
				add(sqh,sqe,snum,cnt,now);
				add(sqh,sqe,snum,now,cnt);
				sqrn[cnt]+=1;
			}
		} else low[now]=min(low[now],dfn[e[i].np]);
	}
}
fx(void,tdp)(int now,int fa){
	if(now<=n) size[now]=1;
	for(R int i=sqh[now];i;i=sqe[i].na){
		if(sqe[i].np==fa) continue;
		tdp(sqe[i].np,now);
		ans+=sqrn[now]*size[now]*size[sqe[i].np]*2;
		size[now]+=size[sqe[i].np];
	}
	ans+=sqrn[now]*size[now]*(ann-size[now])*2;
}
signed main(){
	n=gi(),m=gi();cnt=n;
	for(R int i=1;i<=n;i++) sqrn[i]=-1;
	for(R int i=1;i<=m;i++){
		fr=gi();to=gi();
		add(head,e,num,fr,to);
		add(head,e,num,to,fr);
	}
	for(R int i=1;i<=n;i++){
		if(!dfn[i]){
			ann=0;
			tarjan(i);
			top-=1;
			tdp(i,0);
		}
	}
	printf("%lld
",ans);
}