虚树(Virtual Tree)
与kruskal重构树类似的,虚树也可以说是一种思想而不是一种数据结构或是其他
有一类题目,它会给出很多个点集,然后让你输出每个点集的询问结果
这类题目很大的共性就是所有询问的点集之和并不是很大
对于这样的题目,我们可以利用虚树进行处理
对于平常的虚树紫题,难度不高码量不大,可以在茶余饭后随手一切玩玩
P2495 [SDOI2011]消耗战
题目描述
给定一棵树,边有边权
每次给出一个点集,求使结点 (1) 与给定的点集不连通的最小代价
题目分析
首先如果询问的数量不大,我们可以直接树形dp
设 (f_i) 表示使 (i) 结点与子树中给定的点不连通的最小代价,(S) 表示其子结点集合,(t_i) 表示 (i) 结点是否为给定点集中的点,定义为关键点,(w_{i,j}) 表示连接 (i,j) 两点的边的边权
那么显然有
暴力就做完了,现在考虑 (100\%) 的数据
我们发现,这题所有操作给定的点集大小之和并不是很大
也就是说,很多状态都是冗余的
比如,对于两个关键点(连接这两个关键点的路径上的点都不是关键点),我们很容易发现中间的转移过程都是没有必要的,可以直接计算答案
具体的,答案即为路径上的边权的最小值
例如下图,关键点是 (1,5),那么中间点 (2,3,4) 都是没有必要转移的,我们可以直接预处理,然后树上倍增求出答案

( ext{Figure 1.}) 冗余状态举例
我们考虑给定一个点集之后,哪些点是有用的,哪些点是没有用的
显然,根节点 (1),给定点集中的点都是有用的
还有吗?
观察上面的转移方程可知,两两点的最近公共祖先也是有用的,这也就说明了虚树中不一定只有关键点
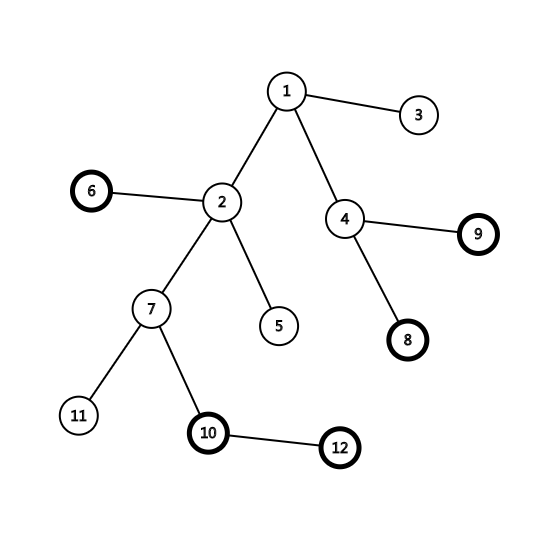
( ext{Figure 2.}) 原树与其关键点
.png)
( ext{Figure 3.}) 原树对应的虚树上的点
然后我们就可以直接去掉没有用的点
对于有用的点的点集,我们不改变他们的祖先关系,重新建树
具体建树的过程的话就是首先按照dfs序排序,一个一个插入,用一个栈来保存
对于这题,两个点之间的权值就是原树中两点之间的路径上的所有边的边权的最小值
树上倍增,对虚树进行dp即可
代码实现
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 600001
#define M 21
#define INF 11000000000000
#define Kafuu return
#define Chino 0
#define R register
#define C const
#define U unsigned
#define fx(l,n) inline l n
#define set(l,n,ty,len) memset(l,n,sizeof(ty)*len)
#define cpy(f,t,ty,len) memcpy(t,f,sizeof(ty)*len)
#define int long long
using namespace std;
struct Tree{
int hs,top,siz,fa,dep,dfn,pre[M],minn[M];
}t[N];
struct Edge{
int w,na,np;
}e[N];
int num,n,u,v,w,head[N],dfnn,stk[N],top,h[N],cnt,lca,m,dp[N];
bool tag[N];
fx(void,add)(int f,int t,int w){
e[++num].na=head[f];
e[num].np=t;e[num].w=w;
head[f]=num;
}
fx(void,dfs1)(int now,int fa,int dep){
t[now].pre[1]=t[now].fa=fa;
t[now].siz=1;t[now].dep=dep;
for(R int i=head[now];i;i=e[i].na){
if(e[i].np==fa) continue;
t[e[i].np].minn[1]=e[i].w;
dfs1(e[i].np,now,dep+1);
t[now].siz+=t[e[i].np].siz;
if(t[e[i].np].siz>t[t[now].hs].siz) t[now].hs=e[i].np;
}
}
fx(void,dfs2)(int now,int top){
t[now].top=top;t[now].dfn=++dfnn;
for(R int i=1;i<21;i++){
if(i>1){
t[now].pre[i]=t[t[now].pre[i-1]].pre[i-1];
t[now].minn[i]=min(t[now].minn[i-1],t[t[now].pre[i-1]].minn[i-1]);}
}
if(!t[now].hs) return;
dfs2(t[now].hs,top);
for(R int i=head[now];i;i=e[i].na){
if(e[i].np==t[now].hs||e[i].np==t[now].fa) continue;
dfs2(e[i].np,e[i].np);
}
}
fx(int,LCA)(int x,int y){
while(t[x].top^t[y].top){
if(t[t[x].top].dep>t[t[y].top].dep) x=t[t[x].top].fa;
else y=t[t[y].top].fa;
}
return t[x].dep>t[y].dep?y:x;
}
fx(int,mindis)(int x,int y){
if(t[x].dep>t[y].dep) swap(x,y);
int dis=INF;
for(R int i=20;i>=1;i--){
if(t[t[y].pre[i]].dep<t[x].dep||!t[y].pre[i]) continue;
dis=min(dis,t[y].minn[i]);y=t[y].pre[i];
if(t[x].dep==t[y].dep) break;
}
return dis;
}
fx(void,ins)(int now){
if(!top){stk[++top]=now;return;}
lca=LCA(stk[top],now);
while(top>1&&t[lca].dep<t[stk[top-1]].dep){
add(stk[top-1],stk[top],mindis(stk[top-1],stk[top]));top-=1;
}
if(t[lca].dep<t[stk[top]].dep) add(lca,stk[top],mindis(lca,stk[top])),top-=1;
if(!top||stk[top]!=lca) stk[++top]=lca;
stk[++top]=now;
}
fx(void,solve)(int now){
for(R int i=head[now];i;i=e[i].na){
solve(e[i].np);
if(tag[e[i].np]) dp[now]+=e[i].w;
else dp[now]+=min(dp[e[i].np],e[i].w);
tag[e[i].np]=0;dp[e[i].np]=0;
}
head[now]=0;
}
fx(int,gi)(){
R char c=getchar();R int s=0,f=1;
while(c>'9'||c<'0'){
if(c=='-') f=-f;
c=getchar();
}
while(c<='9'&&c>='0') s=(s<<3)+(s<<1)+(c-'0'),c=getchar();
return s*f;
}
fx(bool,cmp)(int a,int b){
return t[a].dfn<t[b].dfn;
}
signed main(){
n=gi();
for(R int i=1;i<n;i++){
u=gi(),v=gi(),w=gi();
add(u,v,w);add(v,u,w);
}
dfs1(1,0,1),dfs2(1,1);
for(R int i=1;i<=n;i++) head[i]=0;
m=gi();
while(m--){
cnt=gi();num=0;dp[1]=0;
for(R int i=1;i<=cnt;i++) h[i]=gi(),tag[h[i]]=1;
sort(h+1,h+cnt+1,cmp);
stk[++top]=1;
for(R int i=1;i<=cnt;i++) ins(h[i]);
while(top&&(--top)){
add(stk[top],stk[top+1],mindis(stk[top],stk[top+1]));
}
solve(1);
printf("%lld
",dp[1]);
}
}
CF613D Kingdom and its Cities
题目描述
给定一棵树,同时每次询问给定一个点集,给定点集中的点不能删,求出使给定点集两两不连通的最小删点数量
如果无论如何都会存在两个点连通,输出 (-1)
题目分析
对于这题,无解还是很好判断的
不难发现一个询问无解当且仅当存在至少两个点是父子关系
然后我们仿照上题的套路,建出虚树,然后树形dp
对于两个点如果都是给定点集中的点,那么必须删点
否则就是lca的情况,如果对于这个点的子结点是给定点集中的点的个数超过 (1),那么肯定要删掉这个点,正确性显然
否则上传这个点的子结点中是给定点集中的点的个数
dp完了,这题也就做完了
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 300001
#define M 5001
#define INF 1100000000
#define Kafuu return
#define Chino 0
#define R register
#define C const
#define U unsigned
#define fx(l,n) inline l n
#define set(l,n,ty,len) memset(l,n,sizeof(ty)*len)
#define cpy(f,t,ty,len) memcpy(t,f,sizeof(ty)*len)
using namespace std;
struct Tree{
int dep,hs,siz,dfn,fa,top;
}t[N];
struct Edge{
int na,np;
}e[N];
int n,u,v,dfnn,q,siz[N],cnt,p[N],ans,stk[N],top,lca,head[N],num;
bool nos;
fx(int,gi)(){
R char c=getchar();R int s=0,f=1;
while(c>'9'||c<'0'){
if(c=='-') f=-f;
c=getchar();
}
while(c<='9'&&c>='0') s=(s<<3)+(s<<1)+(c-'0'),c=getchar();
return s*f;
}
fx(void,add)(int f,int t){
e[++num].na=head[f];
e[num].np=t;
head[f]=num;
}
fx(void,dfs1)(int now,int fa,int dep){
t[now].siz=1;t[now].dep=dep;t[now].fa=fa;
for(R int i=head[now];i;i=e[i].na){
if(e[i].np==fa) continue;
dfs1(e[i].np,now,dep+1);
t[now].siz+=t[e[i].np].siz;
if(t[e[i].np].siz>t[t[now].hs].siz) t[now].hs=e[i].np;
}
}
fx(void,dfs2)(int now,int top){
t[now].dfn=++dfnn;t[now].top=top;
if(!t[now].hs) return;
dfs2(t[now].hs,top);
for(R int i=head[now];i;i=e[i].na){
if(e[i].np==t[now].fa||e[i].np==t[now].hs) continue;
dfs2(e[i].np,e[i].np);
}
}
fx(int,LCA)(int x,int y){
while(t[x].top^t[y].top){
if(t[t[x].top].dep>t[t[y].top].dep) x=t[t[x].top].fa;
else y=t[t[y].top].fa;
}
return t[x].dep>t[y].dep?y:x;
}
fx(void,ins)(int now){
if(!top){stk[++top]=now;return;}
lca=LCA(stk[top],now);
while(top>1&&t[lca].dep<t[stk[top-1]].dep){
add(stk[top-1],stk[top]);top-=1;
}
if(t[lca].dep<t[stk[top]].dep) add(lca,stk[top]),top-=1;
if(!top||stk[top]!=lca) stk[++top]=lca;
stk[++top]=now;
}
fx(bool,cmp)(int x,int y){
return t[x].dfn<t[y].dfn;
}
fx(void,solve)(int now){
if(siz[now]){
for(R int i=head[now];i;i=e[i].na){
solve(e[i].np);
if(siz[e[i].np]) siz[e[i].np]=0,ans+=1;
}
} else {
for(R int i=head[now];i;i=e[i].na){
solve(e[i].np);
siz[now]+=siz[e[i].np];
siz[e[i].np]=0;
}
if(siz[now]>1) siz[now]=0,ans+=1;
}
head[now]=0;
}
signed main(){
n=gi();
for(R int i=1;i<n;i++){
u=gi(),v=gi();
add(u,v);add(v,u);
}
dfs1(1,0,1);dfs2(1,1);
for(R int i=1;i<=n;i++) head[i]=0;
q=gi();
while(q--){
cnt=gi();nos=0;ans=0;siz[1]=0;num=0;
for(R int i=1;i<=cnt;i++) p[i]=gi(),siz[p[i]]=1;
for(R int i=1;i<=cnt;i++) if(siz[t[p[i]].fa]) nos=1;
if(nos){
for(R int i=1;i<=cnt;i++) siz[p[i]]=0;
printf("-1
");continue;
}
sort(p+1,p+cnt+1,cmp);
if(p[1]^1) stk[++top]=1;
for(R int i=1;i<=cnt;i++) ins(p[i]);
while(top&&(--top)){
add(stk[top],stk[top+1]);
}
solve(1);
printf("%d
",ans);
}
}
P4103 [HEOI2014]大工程
我怎么老是忘记删掉#include"debug.h"
代码也是大工程啊
题目分析
首先我们考虑代价和,对于点的路径的长度和,并不是很好统计
但是我们可以直接统计每条边被经过了几次
这是一个简单的工作,或是叫简单的组合数学问题,直接做乘法即可
然后我们考虑最小路径长度与最大路径长度
对于每个点,我们维护四个变量:子树中到本点的最短/最长链,子树中满足条件的最大最小值,向上更新即可
顺便说一句,笔者的代码略微麻烦,不建议效仿
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define N 3000001
#define M 5001
#define INF 110000000000
#define Kafuu return
#define Chino 0
#define R register
#define C const
#define U unsigned
#define fx(l,n) inline l n
#define set(l,n,ty,len) memset(l,n,sizeof(ty)*len)
#define cpy(f,t,ty,len) memcpy(t,f,sizeof(ty)*len)
#define int long long
using namespace std;
struct Edge{
int na,np;
}e[N];
struct Tree{
int dep,top,hs,siz,fa,dfn;
}t[N];
struct DP{
int omin,omax,tmax,tmin,tagn;
fx(void,clr)(){omin=omax=tmax=tmin=tagn=0;}
}d[N];
int num,head[N],dfnn,n,m,cnt,k[N],stk[N],top,lca,u,v,tag[N],sum;
fx(void,add)(int f,int t){
e[++num].na=head[f];
e[num].np=t;
head[f]=num;
}
fx(void,dfs1)(int now,int fa,int dep){
t[now].fa=fa,t[now].dep=dep;t[now].siz=1;
for(R int i=head[now];i;i=e[i].na){
if(e[i].np==fa) continue;
dfs1(e[i].np,now,dep+1);
t[now].siz+=t[e[i].np].siz;
if(t[e[i].np].siz>t[t[now].hs].siz) t[now].hs=e[i].np;
}
}
fx(void,dfs2)(int now,int top){
t[now].top=top;t[now].dfn=++dfnn;
if(!t[now].hs) return;
dfs2(t[now].hs,top);
for(R int i=head[now];i;i=e[i].na){
if(e[i].np==t[now].fa||e[i].np==t[now].hs) continue;
dfs2(e[i].np,e[i].np);
}
}
fx(int,LCA)(int x,int y){
while(t[x].top^t[y].top){
if(t[t[x].top].dep>t[t[y].top].dep) x=t[t[x].top].fa;
else y=t[t[y].top].fa;
}
return t[x].dep>t[y].dep?y:x;
}
fx(void,ins)(int now){
if(!top){stk[++top]=now;return;}
lca=LCA(stk[top],now);
while(top>1&&t[lca].dep<t[stk[top-1]].dep){
add(stk[top-1],stk[top]);top-=1;
}
if(t[lca].dep<t[stk[top]].dep) add(lca,stk[top]),top-=1;
if(!top||stk[top]!=lca) stk[++top]=lca;
stk[++top]=now;
}
fx(int,getdis)(int x,int y){
return t[y].dep-t[x].dep;
}
fx(void,solve)(int now){
d[now].omin=d[now].tmin=INF;
d[now].omax=d[now].tmax=-1;
if(tag[now]) d[now].omin=0,d[now].omax=0;
int omi=INF,tmi=INF,oma=-1,tma=-1;
for(R int i=head[now];i;i=e[i].na){
solve(e[i].np);
d[now].tmin=min(d[now].tmin,d[e[i].np].tmin);
d[now].tmax=max(d[now].tmax,d[e[i].np].tmax);
d[e[i].np].omin+=getdis(now,e[i].np);
d[e[i].np].omax+=getdis(now,e[i].np);
d[now].omin=min(d[now].omin,d[e[i].np].omin);
d[now].omax=max(d[now].omax,d[e[i].np].omax);
d[now].tagn+=d[e[i].np].tagn;
sum+=(cnt-d[e[i].np].tagn)*d[e[i].np].tagn*getdis(now,e[i].np);
if(d[e[i].np].omin<omi) tmi=omi,omi=d[e[i].np].omin;
else if(d[e[i].np].omin<tmi) tmi=d[e[i].np].omin;
if(d[e[i].np].omax>oma) tma=oma,oma=d[e[i].np].omax;
else if(d[e[i].np].omax>tma) tma=d[e[i].np].omax;
d[e[i].np].clr();
}
head[now]=0;
if(tag[now]){
d[now].tagn+=1;
d[now].tmin=min(d[now].tmin,omi);
d[now].tmax=max(d[now].tmax,oma);
tag[now]=0;
}
if(omi!=INF&&tmi!=INF) d[now].tmin=min(d[now].tmin,omi+tmi);
if(oma!=-1&&tma!=-1) d[now].tmax=max(d[now].tmax,oma+tma);
}
fx(int,gi)(){
R char c=getchar();R int s=0,f=1;
while(c>'9'||c<'0'){
if(c=='-') f=-f;
c=getchar();
}
while(c<='9'&&c>='0') s=(s<<3)+(s<<1)+(c-'0'),c=getchar();
return s*f;
}
fx(bool,cmp)(int x,int y){
return t[x].dfn<t[y].dfn;
}
signed main(){
n=gi();
for(R int i=1;i<n;i++){
u=gi(),v=gi();
add(u,v);add(v,u);
}
dfs1(1,0,1);dfs2(1,1);
for(R int i=1;i<=n;i++) head[i]=0;
m=gi();
while(m--){
cnt=gi();num=0;d[1].clr();sum=0;
for(R int i=1;i<=cnt;i++) k[i]=gi(),tag[k[i]]=1;
sort(k+1,k+cnt+1,cmp);
if(k[1]^1) stk[++top]=1;
for(R int i=1;i<=cnt;i++) ins(k[i]);
while(top&&(--top)){add(stk[top],stk[top+1]);}
solve(1);
printf("%lld %lld %lld
",sum,d[1].tmin,d[1].tmax);
}
}
[HNOI2014]世界树
说大话了,没切掉QAQ