模型权重初始化的可行性分析

原文链接：https://www.leiphone.com/news/201703/3qMp45aQtbxTdzmK.html

原文是谷歌大神工程师写的一篇文章，看到之后觉得很不错，能够直观地让你深入理解权重初始化方式以及激活函数对模型训练的影响。

本文是对原文的解读，并附上了自己的理解以及代码实现。

首先，一个好的权重初始化方法能够帮助神经网络更快的找到最优解决方案。

初始化权重的必要条件1：各网络层激活值不会落在激活函数的饱和区域；

初始化权重的必要条件2：各网络层激活值不会都非常接近0，也不会都远离0，最好是均值为0（以0为中心分布）

1、初始化为0的可行性：

        不可行，如果将所有的权重都初始化为0，那么所有神经元的输出数值都是一样的，那么反向传播时，同一层的所有的梯度都是一样的，权重更新也是一样的，这样的训练是没有意义的。

2、可行的几种初始化方式：

pre-training:

即是利用训练好的模型的参数进行初始化，然后再做fine-tuning。

Random  initialization:

10层网络，采用随机初始化权重，每层输出数据分布

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
data = tf.constant(np.random.randn(2000, 800),dtype=tf.float32)
layer_sizes = [800 - 50 * i for i in range(0,10)]#10层网络，输入和
num_layers = len(layer_sizes)

fcs = []  # To store fully connected layers' output
for i in range(0, num_layers-1):
    X = data if i == 0 else fcs[i - 1]
    node_in = layer_sizes[i]
    node_out = layer_sizes[i + 1]
   # W = tf.Variable(np.random.randn(node_in, node_out))# * 0.01
    W = tf.Variable(np.random.randn(node_in, node_out),dtype=tf.float32)*0.01
    fc = tf.matmul(X, W)
    fc = tf.nn.tanh(fc)
    fcs.append(fc)


plt.figure()
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(0,num_layers-1):
     plt.subplot(1,num_layers,i+1)
     x=fcs[i]
     x=np.array(x.eval())
     x=x.flatten()
     plt.hist(x=x,bins=20,range=(-1,1))
plt.show()

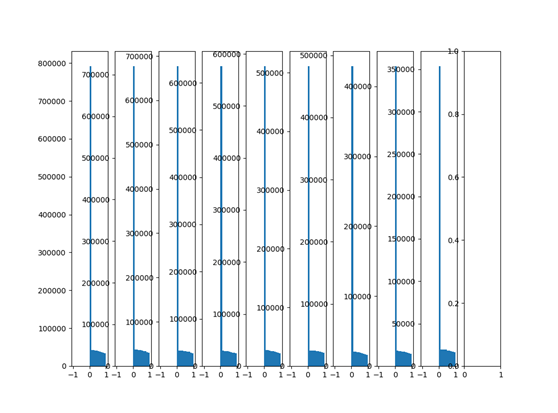
创建10层神经网络，激活函数为tanh,每层权重都采用随机正态分布，均值0，标准差为0.01，以下为输出分布：

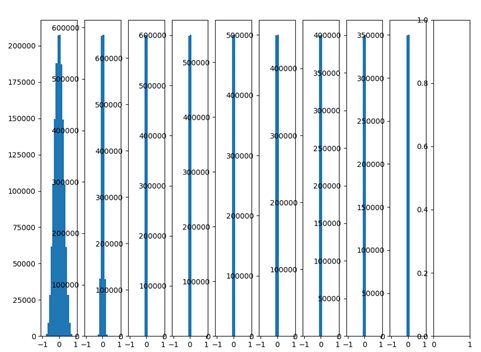
由上图可以看出，随着网络层数的增加，输出数值分布逐渐往0靠近，后面几层输出都非常接近0。根据f=W.X+b可知反向传播时对权重W求偏导时，当前层输出的数值X即是反向传播时计算的梯度中的乘积因子，导致梯度非常小，使得参数更新困难。

将以上正态分布初始化参数值调大，标准差变为1：

W = tf.Variable(np.random.randn(node_in, node_out))

再看看输出分布：

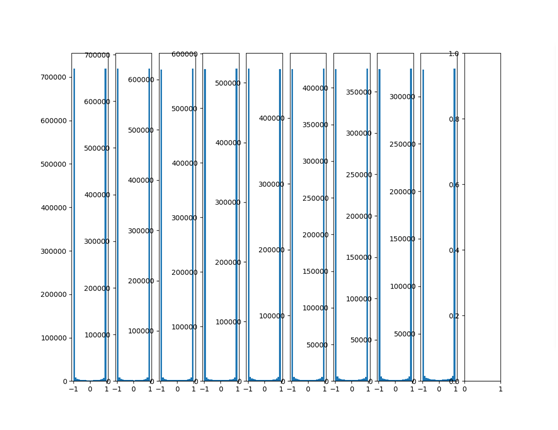
可以看出输出数值都集中在1和-1附近，激活函数用的tanh函数，可见已经落入激活函数的饱和区域，tanh函数1和-1附近的梯度为0，参数难以被更新。

• Xavier initialization

  Xavier initialization 可以解决上面的问题，Xavier初始化是保持输入和输出的方差一致，这样可以避免所有输出值都趋向于0：

• W = tf.Variable(np.random.randn(node_in, node_out)) / np.sqrt(node_in)

  下面就是采用Xavier初始化之后的每层的数据分布直方图：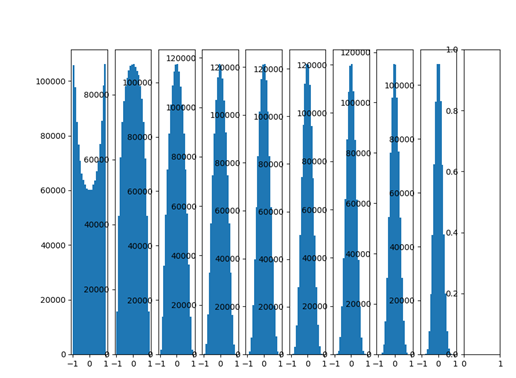

• 

  哇，输出很多层之后依然保持良好的分布，非常有利于我们优化神经网络！

• xavier initialization是在线性函数上推导出来，这说明它对非线性函数并不具有普遍适用性，这里仅仅是讨论了tanh激活函数，下面讨论ReLu激活函数的试验

• 

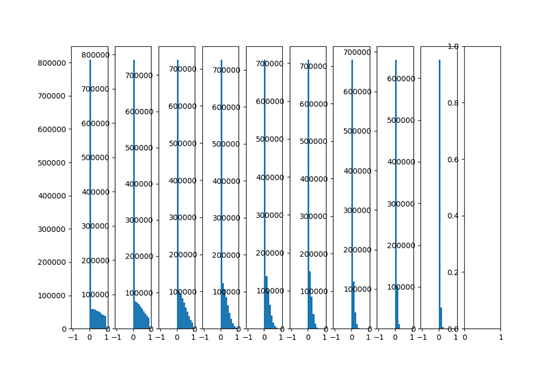
  由上图可以看出，由于relu函数特性导致各层网络数据输出都偏向0-1，输出分布不是zero-centred，且到后面几层，数据都在0附近 。

  看来Xavier初始化对于Relu激活函数不是很适用。下面看看He initialization是否能解决relu初始化问题，He initialization的思想：在relu 网络中，假定每一层有一半的神经元被激活，另一半为0，所以要保持方差不变，只需在Xavier的基础上除以2。

• W = tf.Variable(np.random.randn(node_in, node_out)) / np.sqrt(node_in/2)
  ......

  fc = tf.nn.relu(fc)

下面看看输出分布，虽然不是zero-centred（以0为中心即0均值）但是起码输出数值分布很稳定都在0-1之间，不再像之前用xavier那样在0附近，效果不错，推荐在relu网络中使用。

 

Batch Normalization Layer:

       Batch Normalization是一种巧妙粗暴的方法来削弱不好的initialization带来的影响，想要在非线性激活之前，输出值应该有比较好的分布（例如高斯分布），以便于反向传播计算梯度，更新权重。Batch Normalization将输出值强行做了一次Gaussian Normalization和线性变换。

        Batch Normalization中所有的操作都是平滑可导，这使得反向传播时候可以有效学习到相应的参数Υβ，Bach Normalization 在train 和test时行为有所差别。训练时的

μ_β和σ_β由当前batch计算得出；在testing时μ_β和σ_β应该使用训练时保存的均值或类似的经过处理的值，而不是当前batch计算

Batch Normalization 试验：

Relu激活，随机初始化，无Batch Normal：

随机初始化，有batchNormalization：

 fc=tf.contrib.layers.batch_norm(fc,center=True,scale=True,is_training=True)
#这里注意需要将之前的输入数据，输出数据全部转换成dtype=float32,batchnorm要求数据类型为float32，数据不一致会报错哦

由图上可以看出，加了batch Normalization之后，随着网络的加深，后面几层的输出数据分布仍然保持的很好，没有趋向于0，效果不错。

初始化推荐

            ·在ReLU activation function中推荐使用Xavier Initialization的变种，称之为He Initialization：

                

•   ·使用Batch Normalization layer 可以有效降低深度网络对weight初始化的依赖：
• 

总结：良好的权重初始化和激活函数可以让数据在网络中正常流动，权重正常更新，以达到学习的目的，通过以上实验可以直观的理解权重初始化和激活函数对输出分布的影响。