问题描述
某国的军队由N个部门组成,为了提高安全性,部门之间建立了M条通路,每条通路只能单向传递信息,即一条从部门a到部门b的通路只能由a向b传递信息。信息可以通过中转的方式进行传递,即如果a能将信息传递到b,b又能将信息传递到c,则a能将信息传递到c。一条信息可能通过多次中转最终到达目的地。
由于保密工作做得很好,并不是所有部门之间都互相知道彼此的存在。只有当两个部门之间可以直接或间接传递信息时,他们才彼此知道对方的存在。部门之间不会把自己知道哪些部门告诉其他部门。
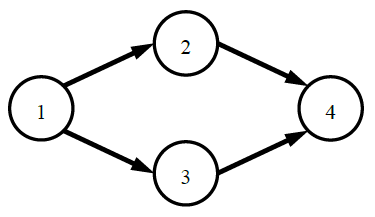
上图中给了一个4个部门的例子,图中的单向边表示通路。部门1可以将消息发送给所有部门,部门4可以接收所有部门的消息,所以部门1和部门4知道所有其他部门的存在。部门2和部门3之间没有任何方式可以发送消息,所以部门2和部门3互相不知道彼此的存在。
现在请问,有多少个部门知道所有N个部门的存在。或者说,有多少个部门所知道的部门数量(包括自己)正好是N。
由于保密工作做得很好,并不是所有部门之间都互相知道彼此的存在。只有当两个部门之间可以直接或间接传递信息时,他们才彼此知道对方的存在。部门之间不会把自己知道哪些部门告诉其他部门。
上图中给了一个4个部门的例子,图中的单向边表示通路。部门1可以将消息发送给所有部门,部门4可以接收所有部门的消息,所以部门1和部门4知道所有其他部门的存在。部门2和部门3之间没有任何方式可以发送消息,所以部门2和部门3互相不知道彼此的存在。
现在请问,有多少个部门知道所有N个部门的存在。或者说,有多少个部门所知道的部门数量(包括自己)正好是N。
输入格式
输入的第一行包含两个整数N, M,分别表示部门的数量和单向通路的数量。所有部门从1到N标号。
接下来M行,每行两个整数a, b,表示部门a到部门b有一条单向通路。
接下来M行,每行两个整数a, b,表示部门a到部门b有一条单向通路。
输出格式
输出一行,包含一个整数,表示答案。
样例输入
4 4
1 2
1 3
2 4
3 4
1 2
1 3
2 4
3 4
样例输出
2
样例说明
部门1和部门4知道所有其他部门的存在。
评测用例规模与约定
对于30%的评测用例,1 ≤ N ≤ 10,1 ≤ M ≤ 20;
对于60%的评测用例,1 ≤ N ≤ 100,1 ≤ M ≤ 1000;
对于100%的评测用例,1 ≤ N ≤ 1000,1 ≤ M ≤ 10000。
对于60%的评测用例,1 ≤ N ≤ 100,1 ≤ M ≤ 1000;
对于100%的评测用例,1 ≤ N ≤ 1000,1 ≤ M ≤ 10000。

枚举每个点,可以到达的点和那些点可以达到他,如果这两个点的集合并是N说明这个点满足题意。
利用反向边计算哪些点可以到达自己。
(用scc找出连通块,然后缩点跑上述算法应该会更快,这里时间足够,当点数过大时不妨考虑这么做)
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define inf 0x3f3f3f3f 4 #define pii pair<int,int> 5 #define mp make_pair 6 #define x first 7 #define y second 8 9 const int maxn=101000; 10 int sum,N,M; 11 bool vis[maxn],tot[maxn]; 12 vector<int>g1[maxn],g2[maxn]; 13 void dfs(int u,int fa,vector<int> g[]){ 14 if(!tot[u]){tot[u]=1;sum++;} 15 vis[u]=1; 16 for(auto v:g[u]){ 17 if(v!=fa&&!vis[v]){ 18 dfs(v,u,g); 19 } 20 } 21 } 22 int main(){ 23 cin>>N>>M; 24 int ans=0,u,v; 25 while(M--){ 26 cin>>u>>v; 27 g1[u].push_back(v); 28 g2[v].push_back(u); 29 } 30 for(int i=1;i<=N;++i){ 31 sum=0; 32 memset(tot,0,sizeof(tot)); 33 memset(vis,0,sizeof(vis)); 34 dfs(i,0,g1); 35 memset(vis,0,sizeof(vis)); 36 dfs(i,0,g2); 37 if(sum==N)ans++; 38 } 39 cout<<ans<<' '; 40 return 0; 41 } 42 /* 43 5 5 44 1 2 45 2 3 46 3 4 47 4 5 48 5 1 49 */