Algorithms

概念
    堆(heap): 
        堆是一个数组, 它可以被看成一个近似的完全二叉树. 树的每一个结点对应数组中的一个元素. 树的根节点是 A[1] 堆包含2个属性 A.length 表示数组A中元素的个数, A.heap_size 表示数组A中存储的堆元素的个数. 也就是说: 虽然 A[1,.., length] 可能都存在数据， 但是只有 A[1,…, heap_size]中存放的属于堆属性的元素.
    
    最大堆, 最小堆(max heap, min heap): 
        最大堆的性质是指除了根以外的所有节点 i 都要满足:
            A[parent(i)] >= A[i]    
        也就是说, 莫个节点的值至多与其父节点一样大.
        
        最小堆正好相反: 
            A[parent(i)] <= A[i]
        
        在排序算法中, 使用的是最大堆。最小堆通常用于构造优先队列。

    
Python programming
　　　

      1 , 各结点下标的维护(父节点 parent, 左子结点 left, 右子结点 right): 

def parent(i):
            return i // 2

        def left(i):
            return 2*i

        def right(i):
            return 2*i + 1  

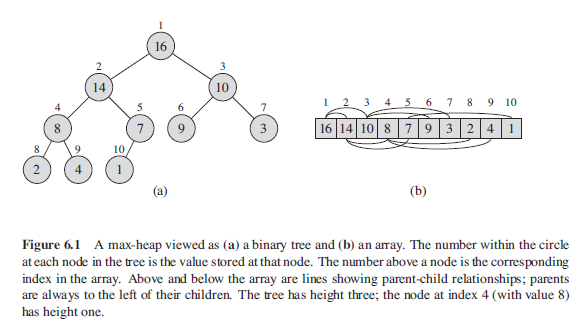
2.  创建 max_heap(A, i) 函数. 它的输入为一个数组A 和一个下标 i. 在函数被调用之前, 假定前提是 left(i) 和 right(i) 都已经是最大堆. 也就是说调用一次 max_heap(A, i), 操作一个A[i]到正确的位置上( i, left(i) 和 right(i) ). 函数通过让 A[i] 值在最大堆中'逐级下降', 从而使得以A[i]为根结点的子树满足最大堆的性质.

def max_heapify(A, i, heap_size): # 这里 heap_size 参数, 而并不是属性实现的.
    l = left(i)
    r = right(i)
    if l <= heap_size and A[l-1] > A[i-1]:
        largest = l
    else:
        largest = i
    if r <= heap_size and A[r-1] > A[largest-1]:
        largest = r
    if largest != i:
        A[i-1], A[largest-1] = A[largest-1], A[i-1]
        max_heapify(A, largest, heap_size)

if __name__ == '__main__':
    A = [16,4,10,14,7,9,3,2,8,1]
    print('Before: ',A)
    max_heapify(A,2,10)
    print('After: ', A)

结果打印:
    Before:  [16, 4, 10, 14, 7, 9, 3, 2, 8, 1]
    After:  [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]

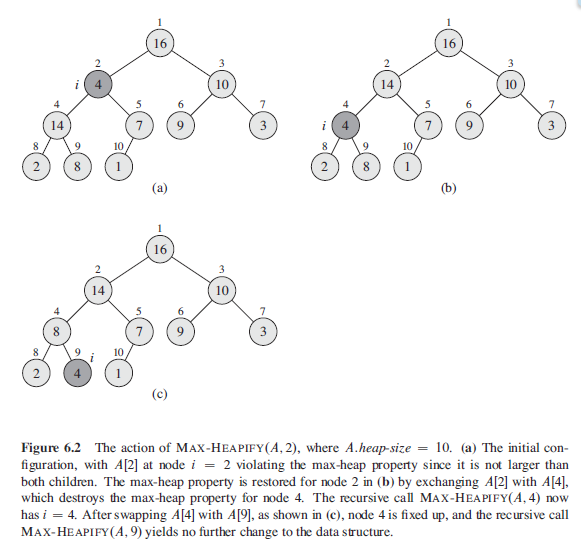
3. 通过 build_max_heap(A) 处理 数组 A 满足最大堆属性.

def build_max_heap(A):
    heap_size = len(A)
    for i in range(1, heap_size//2+1):      # 这里遍历次 heap_size // 2, 因为在函数 max_heapify 已经处理了 heap_size // 2 个元素(通过递归调用的方式)  
        max_heapify(A,heap_size//2 + 1 - i,heap_size)
        print('Factory: ', A)

结果打印:
    Before:  [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
    Factory:  [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
    Factory:  [4, 1, 3, 14, 16, 9, 10, 2, 8, 7]
    Factory:  [4, 1, 10, 14, 16, 9, 3, 2, 8, 7]
    Factory:  [4, 16, 10, 14, 7, 9, 3, 2, 8, 1]
    Factory:  [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
    After:  [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]

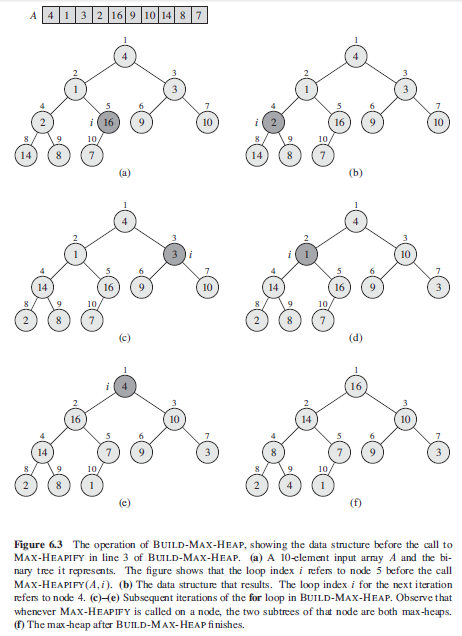
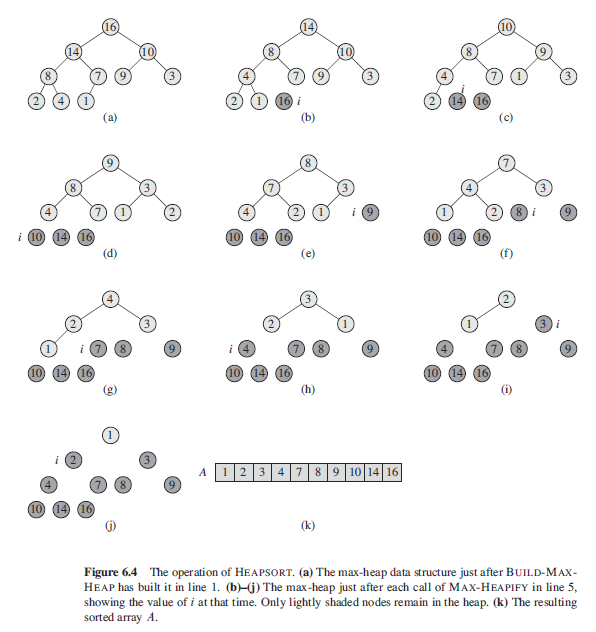
4.  创建 heapsort(A) 函数. 在步骤3中 build_max_heap(A) 将 A 创建成立了最大堆. 这个时候数组A中的最大元素是 A[1], 所以保持将最大堆 A 中的 A[1] 和 A[n]进行互换, 并重复这一互换过程 ( n = n - i, i = [1…, n-2] ), 即可完成了排序. 注意: 每一次互换之前要保证输入数组A的最大堆性质, 这一点可以通过调用 max_heap(A, 1)来保证.

def heap_sort(A):
    build_max_heap(A)
    n = heap_size = len(A)

    for i in range (2, n+1):
        print('Step ', i - 1)
        A[0], A[n-i+1] = A[n-i+1], A[0]
        heap_size -= 1
        max_heapify(A,1, heap_size)
        print(A)

if __name__ == '__main__':
    A = [4,1,3,2,16,9,10,14,8,7]
    print('Before: ', A)
    heap_sort(A)
    print('After: ', A)

结果打印:

Before:  [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
Step  1
    [14, 8, 10, 4, 7, 9, 3, 2, 1, 16]
Step  2
    [10, 8, 9, 4, 7, 1, 3, 2, 14, 16]
Step  3
    [9, 8, 3, 4, 7, 1, 2, 10, 14, 16]
Step  4
    [8, 7, 3, 4, 2, 1, 9, 10, 14, 16]
Step  5
    [7, 4, 3, 1, 2, 8, 9, 10, 14, 16]
Step  6
    [4, 2, 3, 1, 7, 8, 9, 10, 14, 16]
Step  7
    [3, 2, 1, 4, 7, 8, 9, 10, 14, 16]
Step  8
    [2, 1, 3, 4, 7, 8, 9, 10, 14, 16]
Step  9
    [1, 2, 3, 4, 7, 8, 9, 10, 14, 16]
After:  [1, 2, 3, 4, 7, 8, 9, 10, 14, 16] 

Reference, 

　　Introduction to algorithms