CCS

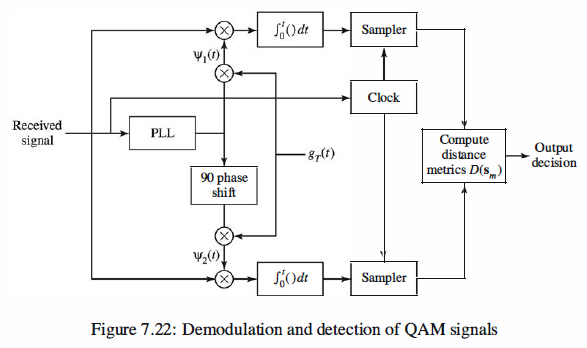
Demodulation and Detection of QAM (Quadrature Amplitude Modulation)

 

Matlab Coding

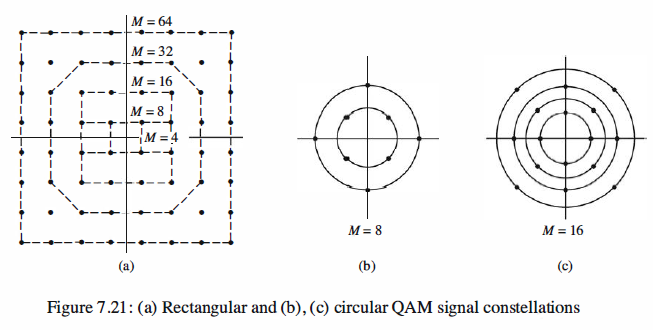
For the M = 8 QAM signal constellation shown in Figure 7.21(b) that 

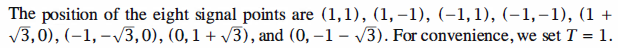
% MATLAB script 

M = 8;
Es = 1;                                 % Energy oer symbol
T = 1;
Ts = 100/T;
fc = 30/T;
t = 0:T/100:T;
l_t = length(t);
A_mc = 1/sqrt(Es);                      % Signal Amplitude
A_ms = -1/sqrt(Es);                     % Signal Amplitude
g_T = sqrt(2/T)*ones(1,l_t);
phi = 2*pi*rand;
si_1 = g_T.*cos(2*pi*fc*t + phi);
si_2 = g_T.*sin(2*pi*fc*t + phi);

var = [ 0 0.05 0.5];                    % Noise variance vector
for k = 1 : length(var)
    % Generation of the noise components:
    n_c = sqrt(var(k))*randn(1,l_t);
    n_s = sqrt(var(k))*randn(1,l_t);
    noise = n_c.*cos(2*pi*fc+t) - n_s.*sin(2*pi*fc+t);
    % The received signal
    r = A_mc*g_T.*cos(2*pi*fc*t+phi) + A_ms*g_T.*sin(2*pi*fc*t+phi) + noise;
    % The correlator outputs:
    y_c = zeros(1,l_t);
    y_s = zeros(1,l_t);
    for i = 1:l_t
        y_c(i) = sum(r(1:i).*si_1(1:i));
        y_s(i) = sum(r(1:i).*si_2(1:i));
    end
    % Plotting the results:
    subplot(3,1,k)
    plot([0 1:length(y_c)-1],y_c,'.-')
    hold
    plot([0 1:length(y_s)-1],y_s)
    title(['sigma^2 = ',num2str(var(k))])
    xlabel('n')
    axis auto
end


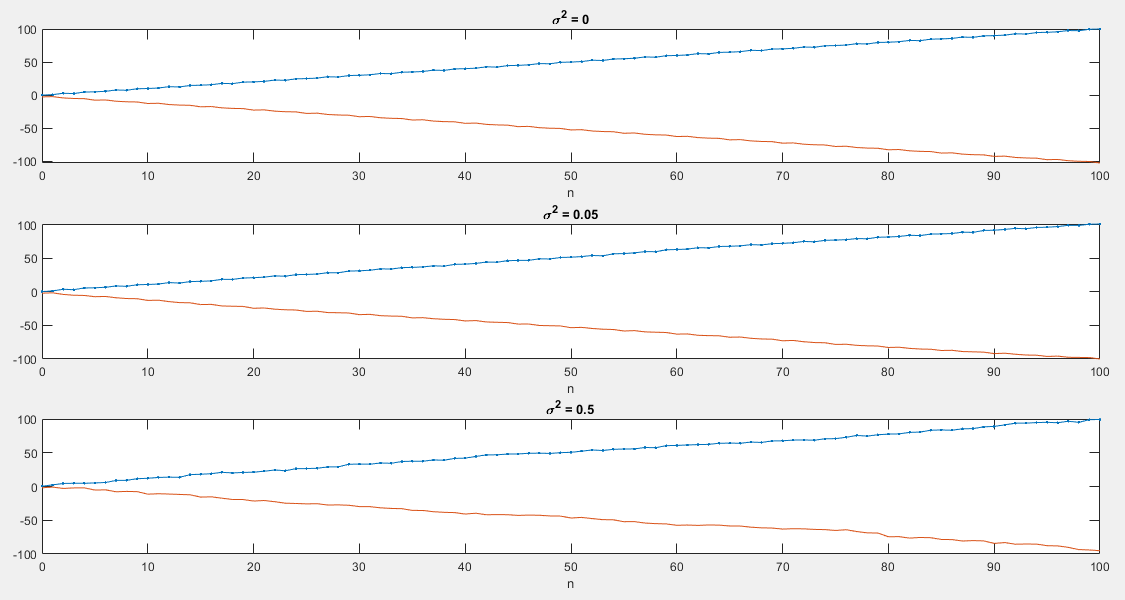
Simulation Result 

Reference,

　　1. <<Contemporary Communication System using MATLAB>> - John G. Proakis