卡特兰数的概念
假如现在有这么一个问题:
一个序列从1到n依次入栈,那么可能的出栈序列一共有多少种?
注意:在任意一个时刻,只要栈不为空,就可能有元素出栈,不是说元素全部入栈之后再出栈。
这个问题的解其实等同于求n阶的卡特兰数(catalan)
卡特兰数指的是在一个n*n的方格中,从左下角走到右上角。每一步只能往右或者往上,且在走的过程中不能越过从左下角到右上角的那条对角线。
和入栈出栈问题对比可以发现,这里的往右走就相当于入栈,往上走就相当于出栈,对角线上的点就相当于栈为空的时候, 不能越过对角线就是说在栈为空的时候不能执行弹栈操作。
出栈序列的求解方法
既然往右相当于入栈, 往上相当于出栈,那么从左下角到右上角的路径即为对应的入栈出栈操作序列,我们可以执行全部的操作序列来获取全部的出栈序列。所以求解出栈序列的个数,只需求出搜索路径有多少个。
当栈深度为4时,所有可能的搜索路径(入栈出栈操作序列):
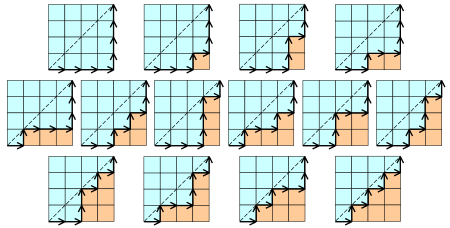
那么搜索又要如何实现?
首先合理的搜索需要满足两个前提:
- 每一步只能往右或者往上
- 且在走的过程中不能越过从左下角到右上角的那条对角线
搜索的递归实现:
- 从某点开始的后续搜索,可以由其上方点的后续搜索和其右方点的后续搜索组成。
#include <stdio.h>
#include <stdlib.h>
void catalan(int push, int pop, int n, char *order) {
int index = push + pop;
if (push == pop && pop == n) {
order[index] = '�';
printf("%s
", order);
}
if (push < n) {
order[index] = 'i';
catalan(push + 1, pop, n, order);
}
if (pop < push) {
order[index] = 'o';
catalan(push, pop + 1, n, order);
}
}
int main() {
// n个数入栈
int n;
scanf("%d", &n);
// 入栈出栈操作序列长为2n;
char *order = calloc(2 * n + 1, sizeof(char));
// 输出所有的入栈出栈操作序列
catalan(0, 0, n, order);
free(order);
return EXIT_SUCCESS;
}
参考链接