最小生成树

最小生成树的算法分为 prim和kruscal算法

初始状态：

设置2个数据结构：

lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST

mst[i]:表示对应lowcost[i]的起点，即说明边<mst[i],i>是MST的一条边，当mst[i]=0表示起点i加入MST

我们假设V1是起始点，进行初始化（*代表无限大，即无通路）：

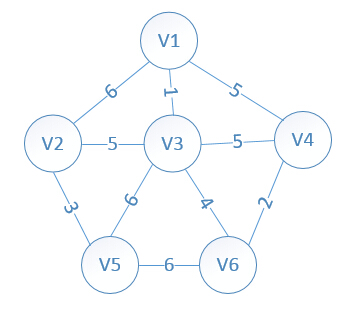
lowcost[2]=6，lowcost[3]=1，lowcost[4]=5，lowcost[5]=*，lowcost[6]=*

mst[2]=1，mst[3]=1，mst[4]=1，mst[5]=1，mst[6]=1，（所有点默认起点是V1）

明显看出，以V3为终点的边的权值最小=1，所以边<mst[3],3>=1加入MST

 

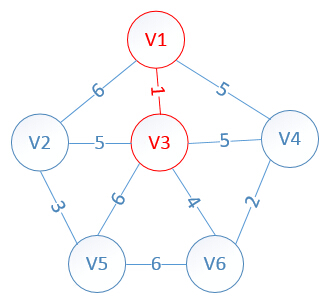
此时，因为点V3的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=5，lowcost[5]=6，lowcost[6]=4

mst[2]=3，mst[3]=0，mst[4]=1，mst[5]=3，mst[6]=3

明显看出，以V6为终点的边的权值最小=4，所以边<mst[6],6>=4加入MST

此时，因为点V6的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=2，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=6，mst[5]=3，mst[6]=0

明显看出，以V4为终点的边的权值最小=2，所以边<mst[4],4>=4加入MST

 

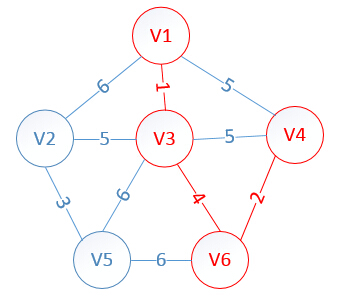
此时，因为点V4的加入，需要更新lowcost数组和mst数组：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=0，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=0，mst[5]=3，mst[6]=0

明显看出，以V2为终点的边的权值最小=5，所以边<mst[2],2>=5加入MST

此时，因为点V2的加入，需要更新lowcost数组和mst数组：

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=3，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=2，mst[6]=0

很明显，以V5为终点的边的权值最小=3，所以边<mst[5],5>=3加入MST

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=0，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=0，mst[6]=0

至此，MST构建成功，如图所示：

#include <iostream>

using namespace std;

#define MAX 100
#define MAXCOST 0xfffffff

int graph[MAX][MAX];
int lowcost[MAX];
int mst[MAX];
int n,sum = 0;

int prim()
{
    int min,minid;
    for (int i=2;i<=n;i++)
    {
        lowcost[i] = graph[1][i];
        mst[i] = 1;
    }
    mst[1] = 0;
    for (int i=2;i<=n;i++)
    {
        min = MAXCOST;
        minid = 0;
        for (int j=2;j<=n;j++)
        {
            if (lowcost[j] < min && lowcost[j]!=0)
            {
                min = lowcost[j];
                minid = j;
            }
        }
        sum += min;
        lowcost[minid] = 0;
        for (int j=2;j<=n;j++)
        {
            if (graph[minid][j] < lowcost[j])
            {
                lowcost[j] = graph[minid][j];
                mst[j] = minid;
            }
        }
    }
    return sum;
}

int main()
{
    int m;
    cin >> n >> m;    // n代表图的顶点，m代表图的边
    //初始化图
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=n;j++)
        {
            graph[i][j] = MAXCOST;
        }
    }
    //构造图
    for (int k=1;k<=m;k++)
    {
        int i,j,cost;
        cin >> i >> j >> cost;
        graph[i][j] = graph[j][i] = cost;
    }
    cout << prim() << endl;
    return 0;
}

kruscal算法 是使用了并查集。始终选择当前可用的最小边权的边（可以直接快排或者algorithm的sort）。每次选择边权最小的边链接两个端点是kruskal的规则，并实时判断两个点之间有没有间接联通。

同样的，模拟过程

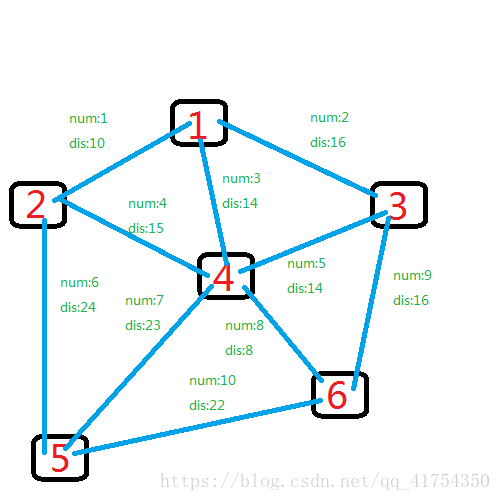
对权值进行排序，随后选取最小对权值的边。

排序后，最小的边自然是第8条边，于是4和6相连

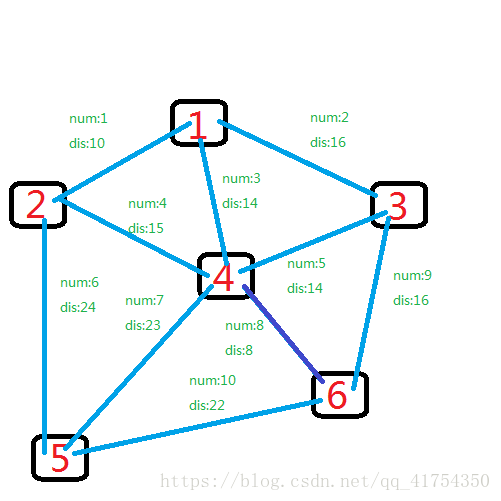
遍历继续，第二小的边是1号，1和2联通。

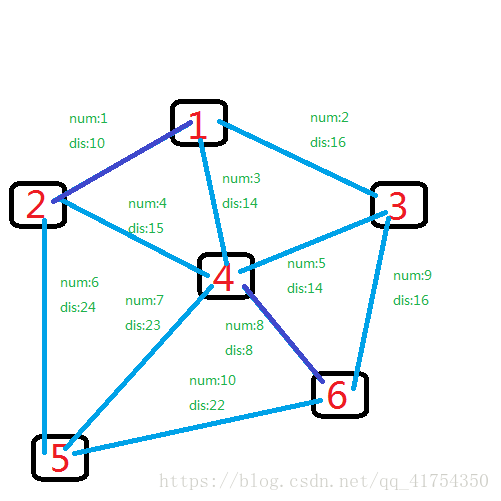
再继续

继续

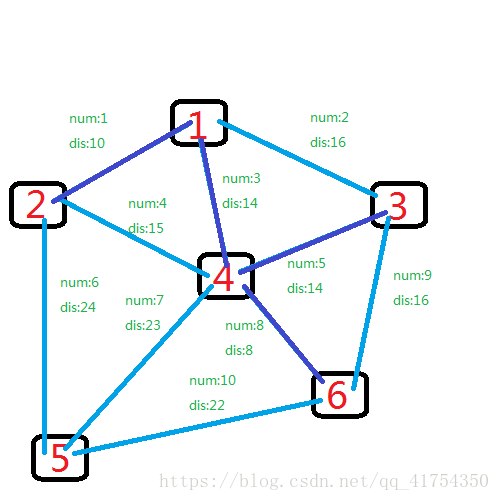
其次是dis为15的边4，但是2和4已经相连了，pass。

然后是dis为16的两条边（边2和边9），边2连接1和3，边9连接3和6，它们都已经间接相连，pass。

再然后就是dis为22的边10，它连接5和6，5还没有加入组织，所以使用这边。继续，发现此时已经连接了n-1条边，结束，最后图示如下：

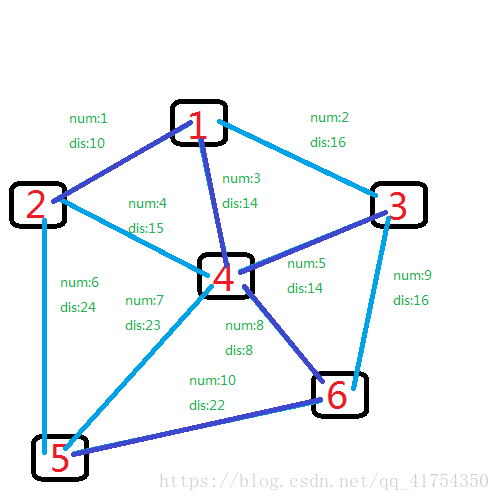
魏队的板子：

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#include <string>
#include <string.h>
#include <vector>
#include <map>
#include <stack>
#include <set>
#include <queue>


#define LL long long
#define INF 0x3f3f3f3f
#define ls nod<<1
#define rs (nod<<1)+1
const int maxn = 2e5+7;
const double eps = 1e-9;

int n,m,ans,cnt,fa[5050];

struct node{
    int u, v, w;
}e[maxn];

bool cmp(node a, node b)
{
    return a.w < b.w;
}

int fid(int x)
{
    return x == fa[x] ? x : fid(fa[x]);
}

bool unite(int r1, int r2)///冰茶鸡
{
    int fidroot1 = fid(r1), fidroot2 = fid(r2);
    if(fidroot1 != fidroot2) {
        fa[fidroot2] = fidroot1;
        return true;
    }
    return false;
}


void init(int n)
{
    for(int i = 1; i <= n; i++) {
        fa[i] = i;
    }
    ans = 0;
    cnt = 0;
}

void kruskal()
{
    std::sort(e+1, e+m+1, cmp);
    for(int i = 1; i <= m; i++) {
        int eu = fid(e[i].u);
        int ev = fid(e[i].v);
        if(eu == ev) {
            continue;
        }
        ans += e[i].w;
        fa[ev] = eu;
        if(++cnt == n-1) {
            break;
        }
    }
}