Nearest Common Ancestors
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 37386 | Accepted: 18694 |
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
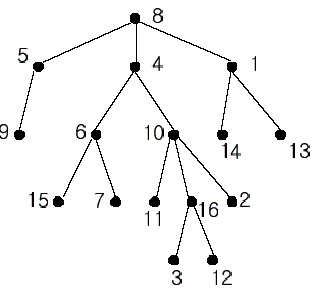
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The
input consists of T test cases. The number of test cases (T) is given in
the first line of the input file. Each test case starts with a line
containing an integer N , the number of nodes in a tree,
2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N.
Each of the next N -1 lines contains a pair of integers that represent
an edge --the first integer is the parent node of the second integer.
Note that a tree with N nodes has exactly N - 1 edges. The last line of
each test case contains two distinct integers whose nearest common
ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2 16 1 14 8 5 10 16 5 9 4 6 8 4 4 10 1 13 6 15 10 11 6 7 10 2 16 3 8 1 16 12 16 7 5 2 3 3 4 3 1 1 5 3 5
Sample Output
4 3
题意:输入t代表有多个测试样例,每个样例第一行输入一个数n,表示有n个节点,接下来n-1行描述这n个节点的关系,第n行输入x,y要求x,y的最近公共祖先
#include <iostream> #include <cstdio> #include <cstring> #include <vector> using namespace std; const int N = 1e4 + 5; vector<int> ve[N];//ve[]是用来建表的一个数组 vector<int> que[N];//que[]是用来查询的一个数组 int ans, pre[N], vis[N];//pre[]是节点编号 int t, n; int find(int x)//查找公共祖先 { return pre[x] == x ? x : find(pre[x]);//距离x最近的一个没有更新父节点的点(pre[x]=x),就是最近的祖先节点 } void init() { for (int i = 1; i <= n; i++) { pre[i] = i;//初始化所有节点的父节点为它本身 vis[i] = 0; ve[i].clear(); que[i].clear(); } } void dfs(int u, int fa) { vis[u] = 1;//标记表示查询过 for (int i = 0; i<ve[u].size(); i++)//借助并查集,在DFS过程中,我们每到达一个节点u,便创建一棵以u为根结点的子树,ve[u].size()就是这个节点子节点的数目 { int v = ve[u][i]; dfs(v, u);//继续以v为子节点,u为根节点往下遍历到底 } for (int j = 0; j<que[u].size(); j++)//反向遍历,更新遍历过节点的父节点 { int v = que[u][j]; if (vis[v] == 1) { ans = find(v); } } pre[u] = fa;//更新父节点 } int main() { scanf("%d", &t); while (t--) { scanf("%d", &n);//是节点数目 init();//初始化 int x, y; for (int i = 0; i<n - 1; i++) //描述父子关系,建表 { scanf("%d %d", &x, &y); ve[x].push_back(y);//父子结点关系,X是父节点,y是子节点 vis[y] = 1;//标记所有子节点,只有最顶上的根节点没有做过子节点才不会被标记 } scanf("%d %d", &x, &y); que[x].push_back(y);//查询 que[y].push_back(x); for (int i = 1; i <= n; i++) { if (vis[i] == 0) { memset(vis, 0, sizeof(vis)); dfs(i, -1);//从根节点开始,因为根节点没有父节点,所以初始为-1 break; } } printf("%d ", ans); } return 0; }