用栈实现队列

问题：

栈和队列在实现上是非常类似的，是否可以用栈实现队列？

问题分析：用栈实现队列等价于用后进先出的特性实现先进先出的特性。

准备两个栈，一个栈用于元素进来，另一个栈用于元素的出去。即从一个栈A中取出数据元素，先放入另一个栈B中，待将栈中A中的数据元素全部放入B中，再从栈B中取出数据元素，经过这么一折腾，这不就由后进先出变成了先进先出嘛。

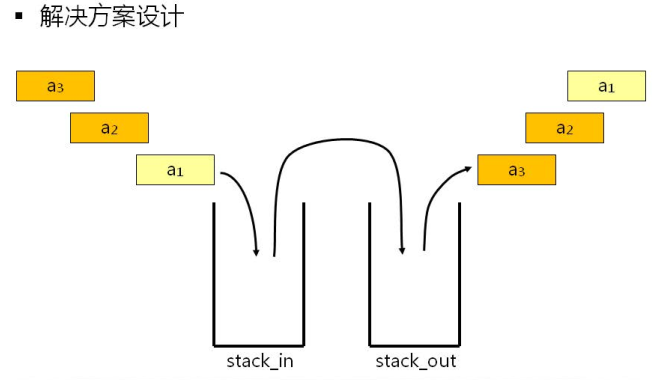
 当stack_out里面没有数据元素的时候，才进行转移。

#include <iostream>
#include "linkstack.h"
#include "LinkQueue.h"

using namespace std;
using namespace DTLib;

template <typename T>
class StatckToQueue : public Queue<T>
{
protected:
    mutable LinkStack<T> m_stack_in;
    mutable LinkStack<T> m_stack_out;
    
    void move() const  //O(n)
    {
        if(m_stack_out.size() == 0)
        {
            while(m_stack_in.size() > 0)
            {
                m_stack_out.push(m_stack_in.top());
                m_stack_in.pop();
            }
        }
    }
public:
    void add(const T& e)   //O(1)
    {
        m_stack_in.push(e);
    }
    void remove()    //O(n)
    {
        move();

        if(m_stack_out.size() > 0)
        {
            m_stack_out.pop();
        }
        else
        {
            THROW_EXCEPTION(InvalidOperationException,"No element in the current queue...");
        }

    }


    T front() const   //O(1)
    {
        move();

        if(m_stack_out.size() > 0)
        {
           return m_stack_out.top();
        }
        else
        {
            THROW_EXCEPTION(InvalidOperationException,"No element in the current queue...");
        }

    }
    void clear()   //O(n)
    {
        m_stack_in.clear();
        m_stack_out.clear();
    }
    int length() const   //O(1)
    {
        return m_stack_in.size() + m_stack_out.size();
    }

};
int main()
{
    StatckToQueue<int> stq;
    for(int i =0; i<10; i++)
    {
        stq.add(i);
    }

    while(stq.length() > 0)
    {
        cout << stq.front() << endl;
        stq.remove();
    }
    return 0;
}

 从打印结果可以看出，确实实现了先进先出的特性。即可以用栈实现队列的先进先出的特性。但是它的性能并不好，因为remove的时间复杂度为O(n)，因此这不是一种好的实现方式，之所以举这个例子，是为了更好的理解栈后进先出和队列先进先出的特性。