2021.5.22 训练赛题解

0. 注

1. 本题解的所有图片和注明内容都可以在 配套文件 之中获得。
2. 所有代码精简，略去了不重要的部分。
3. 部分题目等待更新。

T1.小球

Problem

Solution

...

Code

...

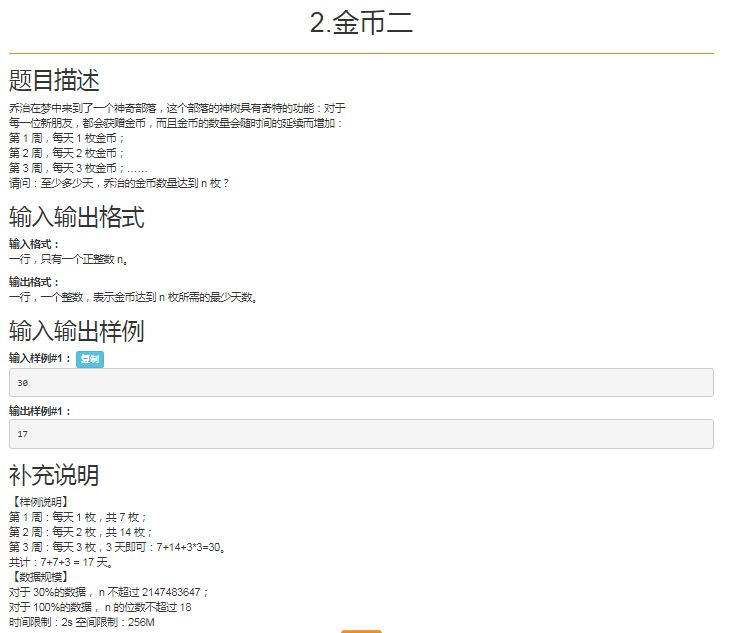
T2.金币二

Problem

Solution

...

Code

...

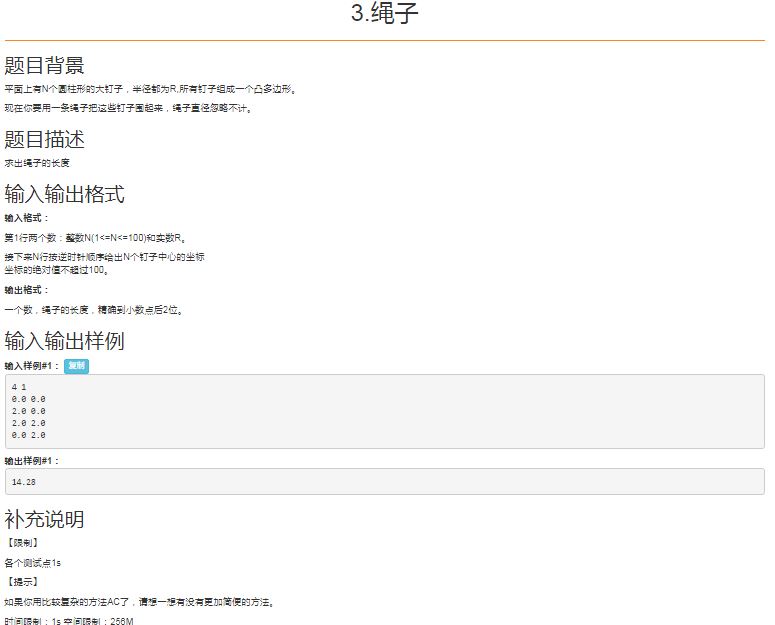
T3.绳子

Problem

Solution

观察题面，是一道明显的几何题。最简单的思想就是模拟，直接去一段一段地求，可这样难免码量过大，考虑有没有简便方法。

从样例入手，可画出图如下 :

（注 : 配套文件中既有图示，也有原使用 GeoGebra 制作的 .ggb 文件）
我们需要用一根绳子把它绕起来，无非就是找一个能覆盖住它的最小周长的多边形。
显然，在四角，最佳方案就是沿着圆弧。
而在其余部分，根据两点之间线段最短，易得最短为连线，即图中所示线段 EG,FJ,IK,HL。
那这个多边形实质上就是一个圆角多边形。
周长可以分为两部分 : 弧与边。
弧四条刚好可以拼成一个整圆，即 (2pi R)。
而边的部分简单观察就可以发现，等于多边形周长。
分开计算并加和即可、
注 : 这里是人为地将每个圆分成了 (4) 个圆心角为 (90^{circ}) 的扇形。

Code

const double pi=3.1415926;
struct information{
	double x;
	double y;	
}a[110]; //结构体直接存储每一个点的坐标 (x,y) 
signed main(){
	int n;
	double r;
	read(n);scanf("%lf",&r);
	for(int i=1;i<=n;i++) scanf("%lf %lf",&a[i].x,&a[i].y);
	double c1=2*pi*r;	//周围 4 段圆弧构成一个整圆的周长 
	double c2=sqrt((a[n].x-a[1].x)*(a[n].x-a[1].x)+(a[n].y-a[1].y)*(a[n].y-a[1].y)); 
	//预处理出 a[n] 与 a[1] 间距离，方便下方循环 
	for(int i=1;i<=n-1;i++) c2=c2+sqrt((a[i].x-a[i+1].x)*(a[i].x-a[i+1].x)+(a[i].y-a[i+1].y)*(a[i].y-a[i+1].y));
	//计算出除 a[n] 与 a[1] 间距离的周长 
	printf("%.2lf",c1+c2);
	return 0;
}

T4.比赛

Problem

Solution

...

Code

...

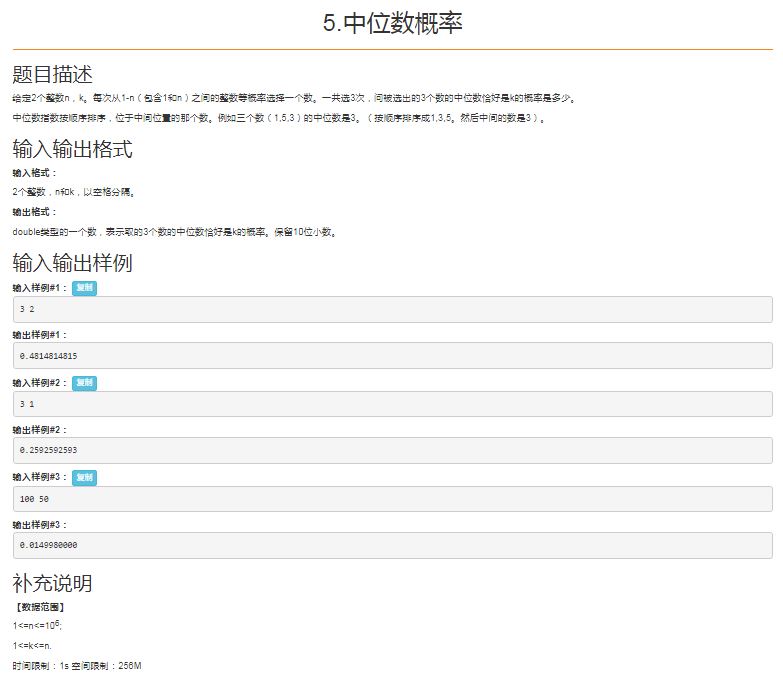
T5.中位数概率

Problem

Solution

显然，这是一道数学题，最简单的方法推公式
回归题目，任取 (3) 个数求中位数是 (k) 的概率是多少。
中位数是由 (3) 个数排序而来的，所以在这之中，一定会有 (1) 个 (k)，这是突破口。
另外两个数取值也颇有讲究，设 (a,b) 为任取的数，(a<k,b>k)
则只有以下几种情况是合法的

• (k) (k) (k)
• (a) (k) (k)
• (b) (k) (k)
• (a) (b) (k)

注意: 这里仅表示取数的情况，不包括排序，即暂时视作无顺序的，来列举所有情况
而考虑顺序（显然选数有先后顺序），有 (1+3+3+6=13) 种情况，将这 (13) 种情况枚举出来，把其概率用 (n) 和 (k) 表示，相加就会有最终的公式。
（样例 1 与样例 2 的取数情况不做展示，文件中有，可自行查看）
不难发现，在 (n) 个数中取到一个 (a) 和一个 (b) 的概率分别是 (dfrac{k-1}{n}) 和 (dfrac{n-k}{n}) ，于是我们有下面这一张表 :

• 取到 (k)
  • 取到比 (k) 大
    • 取到比 (k) 小 概率 (dfrac{(n-k)(k-1)}{n^3})
    • 取到 (k) 概率​ (dfrac{n-k}{n^3})
  • 取到比 (k) 小
    • 取到 (k) 概率 (dfrac{k-1}{n^3})
    • 取到比 (k) 大 概率 (dfrac{(n-k)(k-1)}{n^3})
  • 取到 (k)
    • 取到 (k) (dfrac{1}{n^3})
    • 取到比 (k) 大 概率 (dfrac{n-k}{n^3})
    • 取到比 (k) 小 概率 (dfrac{k-1}{n^3})
• 取到比 (k) 小
  • 取到 (k)
    • 取到 (k) 概率 (dfrac{k-1}{n^3})
    • 取到比 (k) 大 概率 (dfrac{(n-k)(k-1)}{n^3})
  • 取到比 (k) 大
    • 取到 (k) 概率 (dfrac{(n-k)(k-1)}{n^3})
• 取到比 (k) 大
  • 取到 (k)
    • 取到 (k) 概率 (dfrac{n-k}{n^3})
    • 取到比 (k) 小 概率 (dfrac{(n-k)(k-1)}{n^3})
  • 取到比 (k) 小
    • 取到 (k) 概率 (dfrac{(n-k)(k-1)}{n^3})

（注 : 可在文件"T5 k取数分析.md"中获得）

将所有概率相加，可得总概率为 (6(n-k)(k-1)+3n-2)（化简不化简均可），直接带入求值即可。
注意 : 数据类型与范围的选择，double 可以达到 (10^{15})，比同是 (64) 位的 long long 大很多

Code

signed main(){
	int n,k;
	read(n);read(k);
	double a=1.0*6*(n-k)*(k-1)+3*n-2;
	printf("%.10lf",a/n/n/n);
	return 0;
}

signed main(){
	int n,k;
	read(n);read(k);
	double a=1.0*6*n*k-6*k*k+6*k-3*n-2;
	printf("%.10lf",a/n/n/n);
	return 0;
}

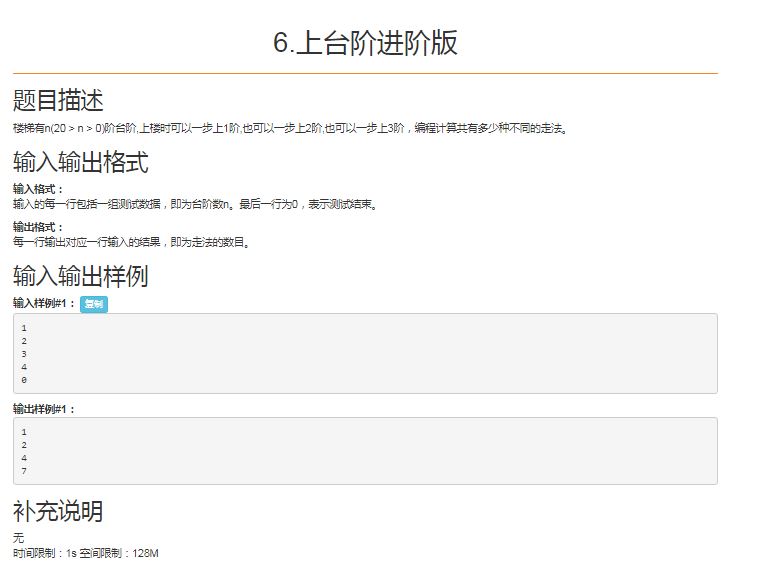
T6.上台阶进阶版

Problem

Solution

典型的一道斐波那契数列的拓展问题。
数据范围很小，直接递推即可。
令 (f[i]) 代表到底第 (i) 级台阶的方案数。
显然有 (f[i]=f[i-1]+f[i-2]+f[i-3] (i>3))
注意初始化 (f[1],f[2],f[3]) ，其余递推即可。

Code

int ff[30];
inline int f(int n){
	for(int i=1;i<=n;i++) ff[i]=max(ff[i],ff[i-1]+ff[i-2]+ff[i-3]);
	return ff[n];
}
signed main(){
	int n;
	ff[1]=1;ff[2]=2;ff[3]=4;
	for(int i=1;;i++){
		read(n);
		if(n==0) return 0;
		printf("%d
",f(n));
	}
	return 0;
}

（注 : 配套文件中有 (nin(0,20)) 的全部数据，可自行查看。）