HDU 1348 Wall 【凸包】

<题目链接>

题目大意:

给出二维坐标轴上 n 个点，这 n 个点构成了一个城堡，国王想建一堵墙，城墙与城堡之间的距离总不小于一个数 L ，求城墙的最小长度，答案四舍五入.

解题分析：

求出这些点所围成的凸包，然后所围城墙的长度就为 该凸包周长 + 以该距离为半径的圆的周长。具体证明如下：

                        

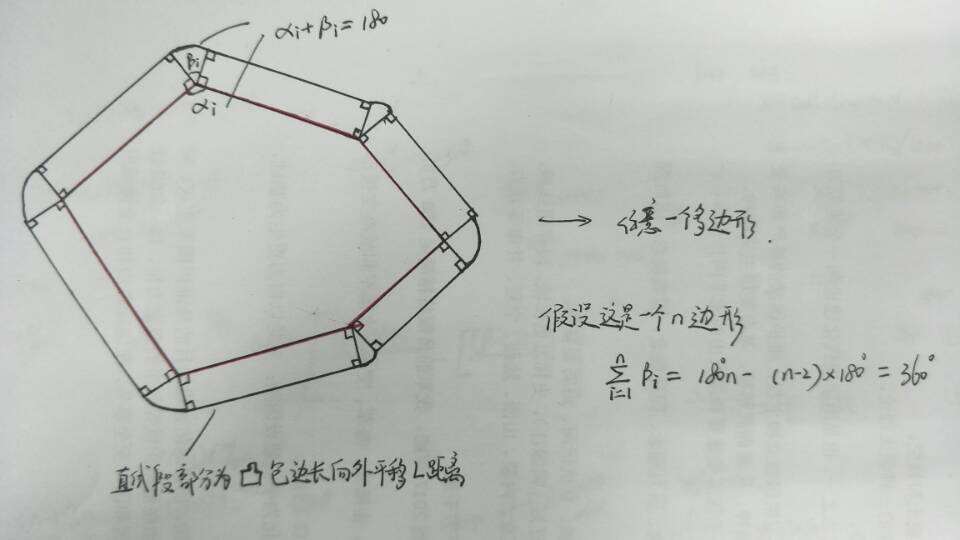
下面的模板还没有整理好

Graham 凸包算法

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define maxn 1100
const double pi = acos(-1.0);

struct Point {
    int x, y;
}s[maxn];

int st[maxn], top;

int cross(Point p, Point p1, Point p2)
{
    return (p1.x - p.x)*(p2.y - p.y) - (p2.x - p.x)*(p1.y - p.y);
}

double dist(Point p1, Point p2)
{
    double tmp = (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y);
    return sqrt(tmp);

}

bool cmp(Point p1, Point p2)
{
    int tmp = cross(s[0], p1, p2);
    if (tmp>0) return true;
    else if (tmp == 0 && dist(s[0], p1)<dist(s[0], p2)) return true;
    else return false;
}

void Graham(int n)
{
    if (n == 1) { top = 0; st[0] = 0; }
    if (n == 2) { top = 1; st[0] = 0; st[1] = 1; }
    if (n>2)
    {
        int i;
        st[0] = 0, st[1] = 1;
        top = 1;
        for (i = 2; i<n; i++)
        {
            while (top>0 && cross(s[st[top - 1]], s[st[top]], s[i])<0)      //不习惯s[st[top-1]]这种代码风格的可以改一下
                top--;
            st[++top] = i;
        }
    }
}

int main()
{
    int n, l;
    int ncase;
    cin >> ncase;
        while (ncase--)
        {
            scanf("%d %d", &n, &l);
            Point p0;
            scanf("%d%d", &s[0].x, &s[0].y);
            p0.x = s[0].x, p0.y = s[0].y;
            int k = 0;
            for (int i = 1; i < n; i++)
            {
                scanf("%d%d", &s[i].x, &s[i].y);
                if ((p0.y > s[i].y) || (p0.y == s[i].y&&p0.x > s[i].x))
                {
                    p0.x = s[i].x;
                    p0.y = s[i].y;
                    k = i;
                }
            }
            s[k] = s[0];
            s[0] = p0;

            sort(s + 1, s + n, cmp);
            Graham(n);
            double ans = 0;
            for (int i = 0; i < top; i++)
            {
                ans += dist(s[st[i]], s[st[i + 1]]);
            }
            ans += dist(s[st[0]], s[st[top]]);
            ans += 2 * pi*l;
            printf("%d
", (int)(ans + 0.5));
            if (ncase)printf("
");
        }
    return 0;
}

Andrew算法

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const double Pi=acos(-1.0);
struct Point{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){}
};
typedef Point Vector;
bool operator < (Point a,Point b){return a.x<b.x||(a.x==b.x&&a.y<b.y);}

Vector operator - (Point a,Point b){return Vector(a.x-b.x,a.y-b.y);}

double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}

double Length(Vector a){return sqrt(Dot(a,a));}

double Angle(Vector a,Vector b){return acos(Dot(a,b)/Length(a)/Length(b));}

Vector Rotate(Vector a,double rad){return Vector(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));}

double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}

Point operator + (Point a,Vector b){return Point(a.x+b.x,a.y+b.y);}

Point getdot(Point a,Vector b,double ang){return a+Rotate(b,ang);}

double getrad(double ang){return Pi*(ang/180);}

Point ans[2500],at[2500];
int nu;


double polygonArea(){
    int k=0;
    for(int i=0;i<nu;i++){
        while(k>1&&Cross(ans[k-1]-ans[k-2],at[i]-ans[k-2])<=0)k--;
        ans[k++]=at[i];
    }
    int p=k;
    for(int i=nu-1;i>=0;i--){
        while(k>p&&Cross(ans[k-1]-ans[k-2],at[i]-ans[k-2])<=0)k--;
        ans[k++]=at[i];
    }
    double x=0;
    k--;
    if(k<2)return 0;

    //求该凸多边形面积
    for(int i=1;i<k-1;i++)x+=Cross(ans[i]-ans[0],ans[i+1]-ans[0]);
    return x/2;
}


int main(){
    int T,n;
    double x,y,w,h,ang;
    scanf("%d",&T);
    while(T--){
        double area1=0,area2=0;
        nu=0;
        scanf("%d",&n);
        while(n--){
            scanf("%lf%lf%lf%lf%lf",&x,&y,&w,&h,&ang);
            area2+=w*h;    //area储存所有矩形的总面积
            Point a;
            ang=-getrad(ang);//因为是顺时针旋转的，所以要是负的。。。。。 
            at[nu++]=getdot(Point(x,y),Vector(w/2,h/2),ang);
            at[nu++]=getdot(Point(x,y),Vector(-w/2,h/2),ang);
            at[nu++]=getdot(Point(x,y),Vector(w/2,-h/2),ang);
            at[nu++]=getdot(Point(x,y),Vector(-w/2,-h/2),ang);
        }
        sort(at,at+nu);
        area1=polygonArea();
    //    printf("%lf %lf
",area1,area2);
        printf("%.1lf %%
",100*area2/area1);
    }
    return 0;
}

2018-08-04