题目链接懒得放了。
题目大意懒得写了。
省选原题哪有找不到的……
说实话,其实这题是个大水题,被我十秒钟内口胡出来了。
首先位运算除了拆位还能干啥?以下以与为例,或是差不多的。
我们考虑有多少个子矩阵会对这一位答案产生贡献,其实就是全 $1$ 的子矩阵。
问题转化为计算全 $1$ 子矩阵的个数。
这是一个简单题。考虑枚举右下角,发现包括这个右下角的子矩阵肯定长这样:(画的比较丑,意会就好了)
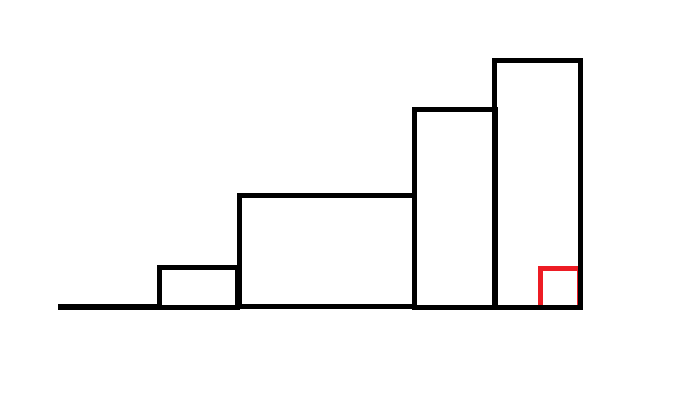
也就是高度单调递增。
高度可以做到 $O(1)$ 转移(从 $h[i-1][j]$)转移。
至于递增的高度,直接一个单调栈。(设为 $s$)
那么这个点为右下角的矩阵个数为 $(s_1-s_0)h[i][s_1]+(s_2-s_1)h[i][s_2]+cdots+(s_{top}-s_{top-1})h[i][s_{top}]$。这个也可以入出栈时随便更新一下。
时间复杂度 $O(n^2log a_i)$。
(然而一开始式子推错了,调了好久,回来再看看发现自己就是个sb……)

#include<bits/stdc++.h> using namespace std; const int maxn=1010,mod=1000000007; #define FOR(i,a,b) for(int i=(a);i<=(b);i++) #define ROF(i,a,b) for(int i=(a);i>=(b);i--) #define MEM(x,v) memset(x,v,sizeof(x)) inline int read(){ char ch=getchar();int x=0,f=0; while(ch<'0' || ch>'9') f|=ch=='-',ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar(); return f?-x:x; } int n,a[maxn][maxn],b[maxn][maxn],ans1,ans2,h[maxn],stk[maxn],tp,sum; int calc1(){ int ans=0; MEM(h,0); FOR(i,1,n){ MEM(stk,0);tp=sum=0; FOR(j,1,n) h[j]=b[i][j]?h[j]+1:0; FOR(j,1,n){ while(tp && h[j]<h[stk[tp]]){ sum=(sum-1ll*h[stk[tp]]*(stk[tp]-stk[tp-1])%mod+mod)%mod; tp--; } stk[++tp]=j; sum=(sum+1ll*h[stk[tp]]*(stk[tp]-stk[tp-1]))%mod; ans=(ans+sum)%mod; } } return ans; } int calc2(){ int ans=0; MEM(h,0); FOR(i,1,n){ MEM(stk,0);tp=sum=0; FOR(j,1,n) h[j]=b[i][j]?0:h[j]+1; FOR(j,1,n){ while(tp && h[j]<h[stk[tp]]){ sum=(sum-1ll*h[stk[tp]]*(stk[tp]-stk[tp-1])%mod+mod)%mod; tp--; } stk[++tp]=j; sum=(sum+1ll*h[stk[tp]]*(stk[tp]-stk[tp-1]))%mod; ans=(ans+sum)%mod; } } int tot=1ll*n*(n+1)*n*(n+1)/4%mod; return (tot-ans+mod)%mod; } int main(){ n=read(); FOR(i,1,n) FOR(j,1,n) a[i][j]=read(); FOR(_,0,30){ FOR(i,1,n) FOR(j,1,n) b[i][j]=(a[i][j]>>_)&1; ans1=(ans1+1ll*calc1()*(1<<_))%mod; ans2=(ans2+1ll*calc2()*(1<<_))%mod; } printf("%d %d ",ans1,ans2); }
