
在上面的数字三角形中寻找一条从顶部到底边的路径,使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可,不必给出具体路径。 三角形的行数大于1小于等于100,数字为 0 - 99
输入格式:
5 //表示三角形的行数 接下来输入三角形
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
要求输出最大和
用递归解决很简单,从上到下遍历一边。
从第一行第一个开始寻找,判断左下或右下哪一个更大,用缓存数组提高效率
1 if (i>=n||j>=n) { 2 return 0; 3 } 4 if (cache[i][j] != -1) { 5 return cache[i][j]; 6 } 7 return cache[i][j]=Math.max(maxSum(i+1, j, n), maxSum(i+1,j+1,n))+num[i][j]; 8
但是递归的效率很慢,不是一个好方法。
那么动态规划呢。
从下至上,首先计算最底层 。底层是无需计算的,保存即可。
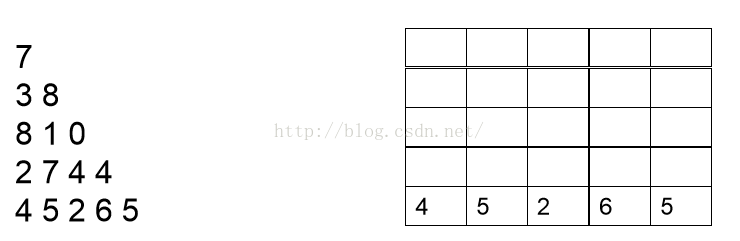
下一步计算倒数第二层。
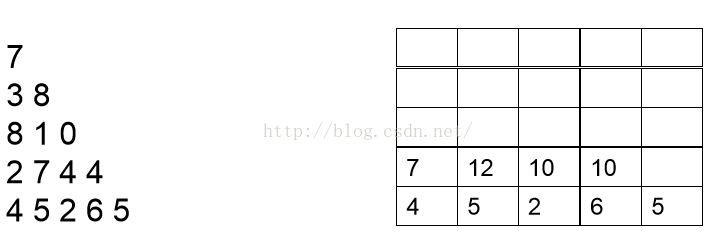
那么用循环就可以很简单的计算出最上面的第一行第一个即为所求
1 public class POJ1163 { 2 public static void main(String[] args) { 3 Scanner sc = new Scanner(System.in); 4 int n = sc.nextInt(); 5 int[][] num = new int[n][n]; 6 int[][] cache = new int[n][n]; 7 int i = 0; 8 while (i < n) { 9 int j = 0; 10 while (j <= i) { 11 num[i][j] = sc.nextInt(); 12 j++; 13 } 14 i++; 15 } 16 for (int j = 0; j < n; j++) { 17 Arrays.fill(cache[j], -1); 18 } 19 long startTime=System.currentTimeMillis(); //获取开始时间 20 System.out.println(maxSum(0,0,n,cache,num)); 21 long endTime=System.currentTimeMillis(); //获取结束时间 22 System.out.println("程序运行时间: "+(endTime-startTime)+"ms"); 23 24 int[][] cal = new int[n][n]; 25 startTime=System.currentTimeMillis(); //获取开始时间 26 for (i = 0; i < n; i++) { 27 cal[n-1][i] = num[n-1][i]; //保存最后一行就可以了 28 } 29 for ( i = n-2; i >= 0; i--) { 30 for (int j = 0; j <= i; j++) { 31 cal[i][j] = Math.max(cal[i+1][j], cal[i+1][j+1])+num[i][j]; 32 } 33 } 34 System.out.println(cal[0][0]); 35 endTime=System.currentTimeMillis(); //获取结束时间 36 System.out.println("程序运行时间: "+(endTime-startTime)+"ms"); 37 38 } 39 public static int maxSum(int i,int j, int n, int[][] cache,int [][] num) { 40 if (i>=n||j>=n) { 41 return 0; 42 } 43 if (cache[i][j] != -1) { 44 return cache[i][j]; 45 } 46 return cache[i][j]=Math.max(maxSum(i+1, j, n,cache,num), maxSum(i+1, j+1,n,cache,num))+num[i][j]; 47 } 48 49 }
还有一种节省空间的方法 用一维数组保存最大值
1 int[] cal1 = new int[n]; 2 for (i = 0; i < n; i++) { 3 cal1[i] = num[n-1][i]; //sikao 4 } 5 for ( i = n-2; i >= 0; i--) { 6 for (int j = 0; j <= i; j++) { 7 cal1[j] = Math.max(cal1[j], cal1[j+1])+num[i][j]; 8 } 9 }
接下来,我们就进行一下总结:
递归到动规的一般转化方法
递归函数有n个参数,就定义一个n维的数组,数组的下标是递归函数参数的取值范围,数组元素的值是递归函数的返回值,这样就可以从边界值开始, 逐步填充数组,相当于计算递归函数值的逆过程。
动规解题的一般思路
1. 将原问题分解为子问题
- 把原问题分解为若干个子问题,子问题和原问题形式相同或类似,只不过规模变小了。子问题都解决,原问题即解决(数字三角形例)。
- 子问题的解一旦求出就会被保存,所以每个子问题只需求 解一次。
2.确定状态
- 在用动态规划解题时,我们往往将和子问题相关的各个变量的一组取值,称之为一个“状 态”。一个“状态”对应于一个或多个子问题, 所谓某个“状态”下的“值”,就是这个“状 态”所对应的子问题的解。
- 所有“状态”的集合,构成问题的“状态空间”。“状态空间”的大小,与用动态规划解决问题的时间复杂度直接相关。 在数字三角形的例子里,一共有N×(N+1)/2个数字,所以这个问题的状态空间里一共就有N×(N+1)/2个状态。
整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。在数字三角形里每个“状态”只需要经过一次,且在每个状态上作计算所花的时间都是和N无关的常数。
3.确定一些初始状态(边界状态)的值
以“数字三角形”为例,初始状态就是底边数字,值就是底边数字值。
4. 确定状态转移方程
定义出什么是“状态”,以及在该“状态”下的“值”后,就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的 “状态”,求出另一个“状态”的“值”(递推型)。状态的迁移可以用递推公式表示,此递推公式也可被称作“状态转移方程”。
数字三角形的状态转移方程:
能用动规解决的问题的特点
1) 问题具有最优子结构性质。如果问题的最优解所包含的 子问题的解也是最优的,我们就称该问题具有最优子结 构性质。
2) 无后效性。当前的若干个状态值一旦确定,则此后过程的演变就只和这若干个状态的值有关,和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态,没有关系。
