Affinity Propagation Demo1学习

利用AP算法进行聚类：

首先导入需要的包：

from sklearn.cluster import AffinityPropagation
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs

生成一组数据：

centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.5, random_state=0)

以上代码包括3个类簇的中心点以及300个以这3个点为中心的样本点。

接下来要利用AP算法对这300个点进行聚类。

af = AffinityPropagation(preference=-50).fit(X) # preference采用负的欧氏距离
cluster_centers_indices = af.cluster_centers_indices_
labels = af.labels_  # 样本标签
n_clusters_ = len(cluster_centers_indices) # 类簇数

打印各种评价指标分数：

print('估计的类簇数: %d' % n_clusters_)
print('Homogeneity: %0.3f' % metrics.homogeneity_score(labels_true, labels))
print('Completeness: %0.3f' %metrics.completeness_score(labels_true, labels))
print('V-measure: %0.3f' %metrics.v_measure_score(labels_true, labels))
print('Adjusted Rand Index:%0.3f' %metrics.adjusted_rand_score(labels_true, labels))
print('Adjusted Mutual Information:%0.3f'%metrics.adjusted_mutual_info_score(labels_true, labels))
print('Silhouette Coefficient:%0.3f' %metrics.silhouette_score(X, labels, metric='sqeuclidean')) # sqeuclidean欧式距离平方

可视化聚类结果：

导入画图需要的包：

import matplotlib.pyplot as plt
from itertools import cycle
plt.close('all')  
plt.figure(1)
plt.clf() # 清除当前图的所有信息
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')

close()方法介绍【可忽略】

close方法简介：

matplotlib.pyplot.close(*args)   --- Close a figure window.
close() by itself closes the current figure

close(fig) closes the Figure instance fig

close(num) closes the figure number num

close(name) where name is a string, closes figure with that label

close('all') closes all the figure windows

for k, col in zip(range(n_clusters_),colors):
    class_members = labels == k;
    print('k:',k)
    print('labels:',labels)
    print('cls_member--------',class_members)
　　cluster_center = X[cluster_centers_indices[k]]
　　print('cluster_center:', cluster_center)
   # 画样本点
　　plt.plot(X[class_members, 0], X[class_members, 1], col + '.')
　　# 画中心点
　　plt.plot(cluster_center[0], cluster_center[1], 'o',
         markeredgecolor='k', markersize=28)
　　
# 划线
　　for x in X[class_members]:
   　　 plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col)
 

plt.title('Estimated number of clusters:%d' %n_clusters_)
plt.show()# 显示图

运行结果：

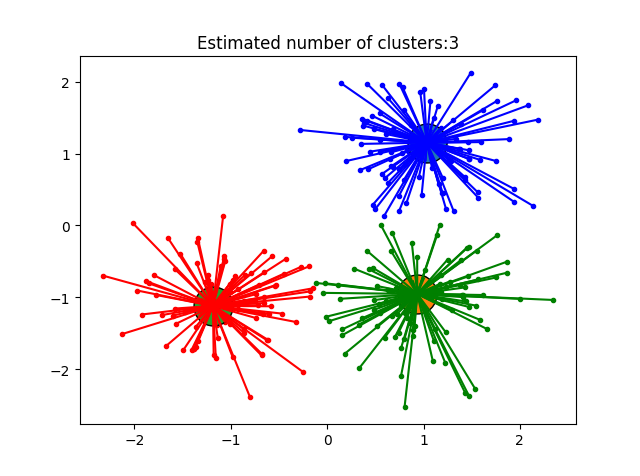
完整代码：

print(__doc__)

from sklearn.cluster import AffinityPropagation
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs

# #################################################
# generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.5, random_state=0)

# #######################################################
# Compute Affinity Propagation
af = AffinityPropagation(preference=-50).fit(X) # preference采用负的欧氏距离
cluster_centers_indices = af.cluster_centers_indices_
labels = af.labels_  # 样本标签

n_clusters_ = len(cluster_centers_indices) # 类簇数

print('估计的类簇数: %d' % n_clusters_)
print('Homogeneity: %0.3f' % metrics.homogeneity_score(labels_true, labels))
print('Completeness: %0.3f' %metrics.completeness_score(labels_true, labels))
print('V-measure: %0.3f' %metrics.v_measure_score(labels_true, labels))
print('Adjusted Rand Index:%0.3f' %metrics.adjusted_rand_score(labels_true, labels))
print('Adjusted Mutual Information:%0.3f'%metrics.adjusted_mutual_info_score(labels_true, labels))
print('Silhouette Coefficient:%0.3f' %metrics.silhouette_score(X, labels, metric='sqeuclidean')) # sqeuclidean欧式距离平方

# ##########################################################
# Plot result
import matplotlib.pyplot as plt
from itertools import cycle

plt.close('all')
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_),colors):
    class_members = labels == k;
    print('k:',k)
    print('labels:',labels)
    print('cls_member--------',class_members)

    cluster_center = X[cluster_centers_indices[k]]
    print('cluster_center:', cluster_center)
    plt.plot(X[class_members, 0], X[class_members, 1], col + '.')
    plt.plot(cluster_center[0], cluster_center[1], 'o',
             markeredgecolor='k', markersize=28)

    # 划线
    for x in X[class_members]:
        plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col)

plt.title('Estimated number of clusters:%d' %n_clusters_)
plt.show()