搜索------深度优先DFS-----模板2：例1 例2 例3 例4

 void   DFS(int k)  //处理第k步
{    for (int i=1; i<=m; i++)  //第k步中有m种可能
     {      处理第k步
                 if  (k==n)    //已经处理完n步，到达目的状态 
             {     输出结果；       return；       }
             DFS(k+1)；              //进入第k+1步
     }
}

例1：多重排列问题

输出1-m个数中取n个数的所有多重排列。

例如n=2，m=3的所有多重排列为：
1    1
1    2
1    3
2    1
2    2
2    3
3    1
3    2
3    3

//从1到m中取n个数，允许重复取数

#include <iostream>
using namespace std;
int n,m, a[10];
void  DFS(int k)
{      for (int i=1; i<=m; i++)   
       {    a[k]=i;    
            if  (k==n) 
            {   for (int i=0; i<n; i++)     cout<<a[i]<<" ";
                cout<<endl;   return;  
            }
            DFS(k+1);      
       } 
}
int main()
{        cin>>m>>n;         DFS(0);    return 0;       }

//从1到m中取n个数，允许重复取数

#include <iostream>

using namespace std;

int n,m, a[10];

void  DFS(int k)

{      for (int i=1; i<=m; i++)

          {    a[k]=i;        

                       if  (k==n)

                                   {   for (int i=0; i<n; i++)     cout<<a[i]<<" ";

                                                                         cout<<endl;   return;              }

            DFS(k+1);            

                }

}

int main()

{   

     cin>>m>>n; 

        DFS(0);

    return 0;  

     }

例2：排列问题

输出1-m个数中取n个数的所有排列。例如m=3 ，n=2的所有排列为：
1    2
1    3
2    1
2    3
3    1
3    2

//从1到m中取n个数，不允许重复取数
#include <iostream>
using namespace std;
int n,m, a[10];  bool bz[10];
void  DFS(int k)
{     for (int i=1; i<=m; i++)   
            if ( !bz[i] )
            {     a[k]=i; 
                   if  (k==n) 
                   {    for (int i=0; i<n; i++)     cout<<a[i]<<" ";
                         cout<<endl;   return;
                   } 
                   bz[i]=true;  DFS(k+1); bz[i]=false;
           }       
}
int main()
{   cin>>m>>n;    
    for (int i=0; i<m; i++) a[i]=i+1;
    DFS(0);   return 0;    
}

//从1到m中取n个数，不允许重复取数
#include <iostream>
using namespace std;
int n,m, a[10];  bool bz[10];
void  DFS(int k)
{     for (int i=1; i<=m; i++)  
            if ( !bz[i] )
            {     a[k]=i;
                   if  (k==n)
                   {    for (int i=0; i<n; i++)     cout<<a[i]<<" ";
                         cout<<endl;   return;
                   }
                   bz[i]=true;  DFS(k+1); bz[i]=false;
           }      
}
int main()
{   cin>>m>>n;   
    for (int i=0; i<m; i++) a[i]=i+1;
    DFS(0);   return 0;   
}

//从1到m中取n个数，不允许重复取数
#include <iostream>
using namespace std;
int n,m, a[10];
void  DFS(int k)
{      for (int i=k; i<m; i++)   
       {     if  (k==n) 
             {      for (int i=0; i<n; i++)     cout<<a[i]<<" ";
                    cout<<endl;  return ;  
             }
            int t=a[k];a[k]=a[i];a[i]=t;    
            DFS(k+1); 
            t=a[k];a[k]=a[i];a[i]=t;       
       }
}
int main()
{        cin>>m>>n;         DFS(0);    return 0;       }

//从1到m中取n个数，不允许重复取数
#include <iostream>
using namespace std;
int n,m, a[10];
void  DFS(int k)
{      for (int i=k; i<m; i++)  
       {     if  (k==n)
             {      for (int i=0; i<n; i++)     cout<<a[i]<<" ";
                    cout<<endl;  return ; 
             }
            int t=a[k];a[k]=a[i];a[i]=t;   
            DFS(k+1);
            t=a[k];a[k]=a[i];a[i]=t;      
       }
}
int main()
{        cin>>m>>n;         DFS(0);    return 0;       }

例3：组合问题

输出m个数中取n个数的所有组合。例如m=5，n=3的所有组合为：
1      2      3
1      2      4
1      2      5
1      3      4
1      3      5
1      4      5
2      3      4
2      3      5
2      4      5
3      4      5

#include<iostream>
using namespace std;

int m,n,a[10];  //存放每个数
void comb(int k)
{      for (int i=a[k-1]+1; i<=m-n+k; i++)
       {     a[k]=i;
         if ( k>n ) 
              {      for (int i=1; i<=n;i++) printf("%5d",a[i]);
          printf("
");          return;
               }
         comb(k+1); 
        }
}
int main( )  
{    scanf("%d%d",&m,&n);
    comb(1);  //从第1个数开始
 }

#include<iostream> using namespace std;

int m,n,a[10];  //存放每个数

void comb(int k)

{ 

     for (int i=a[k-1]+1; i<=m-n+k; i++)

       {     a[k]=i;   

                    if ( k>n )  

               {             for (int i=1; i<=n;i++)        printf("%5d",a[i]);

                                             printf(" ");          return;            

                      }  

     comb(k+1);

        }

}

int main( )

  {

 scanf("%d%d",&m,&n);

 comb(1);  //从第1个数开始

 }

 例4：0-1背包问题回溯求解

有不同价值、不同重量的物品n件，

求从这n件物品中选取一部分物品的选择方案，

使选中物品的总重量不超过指定的限制重量，但选中物品的价值之和最大。

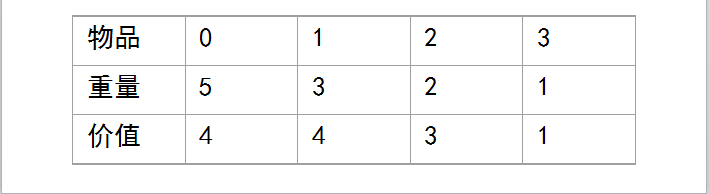
例如：设限制重量为7，现有4件物品，它们的重量和价值见下表，问如何物品的价值之和最大？

// 0-1背包问题的回溯算法：
#include <stdio.h>
#define M 10
int w[M]={5,3,2,1}, v[M]={4,4,3,1}, limit_w=7, n=4; 
int   tw=0, maxv=0, tv=0, b[M]={0} ;
void find(int i)   
{    if (i==n) return;    //已对所有物品作了判断
    if (tw+w[i]<=limit_w )   //选择第i件物品
        if (i<=n-1)    //进入第i+1件的条件
        {    tw=tw+w[i]; tv=tv+v[i]; b[i]=1; //选了第i件
        if (maxv<tv)  maxv=tv;
        find(i+1); //进入第i+1件
        tw=tw-w[i]; tv=tv-v[i]; b[i]=0;   //不选第i件了
        }
     if (i<=n-1) find(i+1);  //不选择第i件物品
}
void main( )
{    find(0); //从第0件物品开始选择
    printf("maxv=%d
",maxv);  }

// 0-1背包问题的回溯算法：
#include <stdio.h>
#define M 10
int w[M]={5,3,2,1}, v[M]={4,4,3,1}, limit_w=7, n=4;

int   tw=0, maxv=0, tv=0, b[M]={0} ;

void find(int i)  
{ if (i==n) return;    //已对所有物品作了判断
 if (tw+w[i]<=limit_w )   //选择第i件物品
     if (i<=n-1)    //进入第i+1件的条件

     {             tw=tw+w[i];          tv=tv+v[i];           b[i]=1;  //选了第i件
  if (maxv<tv)               maxv=tv;
                    find(i+1); //进入第i+1件
  tw=tw-w[i];               tv=tv-v[i];        b[i]=0;    //不选第i件了
     }

  if (i<=n-1) find(i+1);  //不选择第i件物品
}

void main( )
{             find(0); //从第0件物品开始选择

 printf("maxv=%d ",maxv);                  }