递归函数 是能够直接或通过另一个函数间接调用自身的函数,调用自身的方法称为递归调用。递归调用的本质是使用同一算法将复杂的问题不断化简,直到该问题解决。
例如求斐波那契数列的某一项算法适用于递归函数实现。斐波那契数列指的是这样一个数列:
0, 1, 1, 2, 3, 5, 8, 13, 21 ...
这个数列从第三项开始,每一项都等于前两项之和。斐波那契数列可以按照如下公式递归定义;
fibonacci(0) = 0 // 处理 0 fibonacci(1) = 1 // 处理 1 fibonacci(n) = fibonacci(n - 1) + fibonacci(n -2) // 处理 1 意外的自然数
完整的程序如下所示:
long fibonacci(long n)
{
if ( n == 1 || n == 2)
{
return n;
}
else
{
return fibonacci(n - 1) + fibonacci(n -2);
// 递归调用自身,将当前问题分解为 2 个分支
}
}
int main()
{
long n; // 声明长整型变量,用于保存要斐波那契数列项数
puts("请输入一个正整数:"); // 输出提示信息
scanf("%d", n); // 输入变量 n 的值
printf(斐波那契数列第 %d 项为:%d", n, fibonacci(n)); // 调用 fibonacci()函数
}
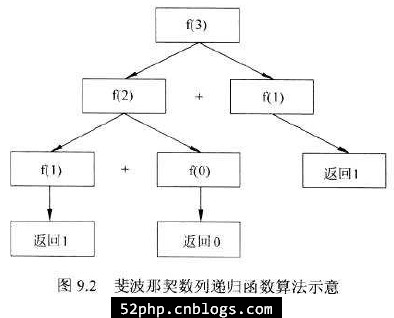
main() 函数调用 fibonacci() 函数对自身递归调用。每次调用时,它会判断 n 是否为 0 或者 1。如果条件为真,则返回 n,结束当前函数。如果 n 大于 1,那么函数会生成 2 个递归调用,每个递归调用相比原始的 fibonacci() 函数调用都会更简单,如图 9.2 所示。