Fibonacci 数列算法分析

/*************************************************
*  Fibonacci 数列算法分析
*************************************************/
#include<iostream>
#include<stdio.h>
#include<vector>
#include<cmath>
#include<time.h>
using namespace std;
#define Time 1000000
#define N 15
#define Echo printf("result：%d | spend：%.3f
",a,(((double)(clock()-start))/1000))
#define For for(int i=1; i<Time; ++i)
/*************************************************
Function:       fibo1 fibo2 fibo3  fibo4
defferent:      1递归 2迭代 3向量 4公式
Description:    斐波那契数列求值
Return:         返回第N项的值
*************************************************/
int fibo1(int n) {
    if(n==0)return 0;
    if(n==1)return 1;
    return fibo1(n-1)+fibo1(n-2);
}
int fibo2(int n) {
    int a=0,c;
    for(int b=1,i=2; i<=n; ++i)
        c=a+b,a=b,b=c;
    return c;
}
int fibo3(int n) {
    vector<int> v(n+1,0);
    v[1]=1;
    for(int i=2; i<=n; ++i)
        v[i]=v[i-1]+v[i-2];
    return v[n];
}
int fibo4(int n) {
    return (pow((1+sqrt(5.0))/2,n)-pow((1-sqrt(5.0))/2,n))/sqrt(5.0);
}

int main() {
    int a;

    clock_t start=clock();
    For a=fibo1(N);
    Echo;

    start=clock();
    For a=fibo2(N);
    Echo;

    start=clock();
    For a=fibo3(N);
    Echo;

    start=clock();
    For a=fibo4(N);
    Echo;

    return 0;
}

循环次数 100000 ，N 为 10 结果如下  

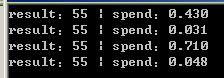
循环次数 100000 ，N 为 15 结果如下  

 -循环次数 100000 ，N 为 20 结果如下  

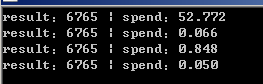
可以看出递归最为耗时：代码简单易懂

向量由于做了大量的下标工作，相对来说次之

公式法再次之（在N=15时，公式法与迭代法性能不确定）：公式推导，性能具有良好的稳定性

迭代最优：编程复杂，效率较高

以上只是针对本次测试