简介
此算法是基于高斯消元的基础上改进而成的,唯一不同之处是多进行了几次矩阵变换使得化为行最简型矩阵。相比于高斯消元法此方法效率较低,但是不需要回带求解。
此算法的过程大概为:首先确定每个 \(a_{i,j}\) 不为 \(0\)(如果为 \(0\) 就和下面的行替换),接着将每个 \(a_{i,j}\) 通过行变换化为 \(1\)(该行都除以 \(a_{i,j}\)),然后通过行变换将每列除了 \(a_{i,i}\) 以外的都消成 \(0\),重复 \(n\) 次即可。
推演
如下是一个求解过程的示例:
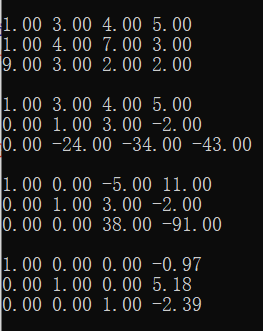
首先最简单的操作是输入增广矩阵:
for(int i=1; i<=n; i++) {
for(int j=1; j<=n+1; j++) {
scanf("%lf",a[i]+j);
}
}
接下来开始消元的第一步:判断是否有解。
我们每次考虑 \(a_{i,j}\),先看该列的元素是否全为 \(0\)。第二次以后时我们都没有考虑该列上面得到元素,因为他们已经可以被化简为 \(0\)。
int max=i;
for(int j=i+1; j<=n; j++) {
if(fabs(a[j][i])>fabs(a[max][i])) {
max=j;
}
}
消元的第二步:找到该列第一个非零元素后将该行和第 \(i\) 行元素作行交换。我们上面判断是否有解实际上是在找第i ii列第一个非零元素。
for(int j=1; j<=n+1; j++) {
swap(a[i][j],a[max][j]);
}
消元的第三步:将第 \(i\) 行第 \(i\) 列的元素化为 \(1\),将第 \(i\) 列除了第 \(i\) 行的元素全消成 \(0\)。方法是第 \(j\) 行每个元素 \(a_{j,k}\) 都减去 \(a_{j,k}\times a_{i,k}\) ,将当前行的所有元素都除以 \(a_{i,j}\)。
for(int j=1; j<=n; j++) {
if(j^i) {
D temp=a[j][i]/a[i][i];
for(int k=i+1; k<=n+1; k++) {
a[j][k]-=a[i][k]*temp;
}
}
}
如果有多个解的情况呢?如果某变量有多个解,那么第 \(i\) 行的第 \(i\) 个数一定都等于 \(0\)。
下面是存在一个通解并且将其设置为1的例子:
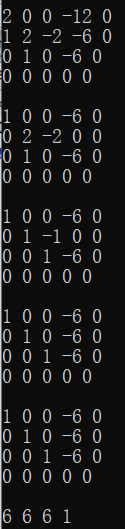
其实上面三步写在一个 for 循环即可,因此得到该代码:
for(int i=1; i<=n; i++) {
for(int j=1; j<=n+1; j++) {
scanf("%lf",a[i]+j);
}
}
for(int i=1; i<=n; i++) {
int max=i;
for(int j=i+1; j<=n; j++) {
if(fabs(a[j][i])>fabs(a[max][i])) {
max=j;
}
}
for(int j=1; j<=n+1; j++) {
swap(a[i][j],a[max][j]);
}
if(fabs(a[i][i])<eps) {
puts("No Solution");
return 0;
}
for(int j=1; j<=n; j++) {
if(j^i) {
D temp=a[j][i]/a[i][i];
for(int k=i+1; k<=n+1; k++) {
a[j][k]-=a[i][k]*temp;
}
}
}
}
