hdu 1695(莫比乌斯反演）

GCD

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 12004    Accepted Submission(s): 4531

Problem Description

Given 5 integers: a, b, c, d, k, you're to find x in a...b, y in c...d that GCD(x, y) = k. GCD(x, y) means the greatest common divisor of x and y. Since the number of choices may be very large, you're only required to output the total number of different number pairs.
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.

Yoiu can assume that a = c = 1 in all test cases.

 

Input

The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 3,000 cases.
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.

 

Output

For each test case, print the number of choices. Use the format in the example.

 

Sample Input

2 1 3 1 5 1 1 11014 1 14409 9

 

Sample Output

Case 1: 9 Case 2: 736427

Hint

For the first sample input, all the 9 pairs of numbers are (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 5), (3, 4), (3, 5).

 

Source

2008 “Sunline Cup” National Invitational Contest

题意：在[a,b]里面选一个数x，[c,d]里面选一个数y 使得gcd(x,y)==k,这样的方案有多少个

定义：

f(d)表示gcd（x,y)==k的个数  演化就是gcd(x/k,y/k)==1的个数

F(n)表示gcd(x/k,y/k)==n(t=1,2,3,4,5,...)

可以通过莫比乌斯反演变化为    

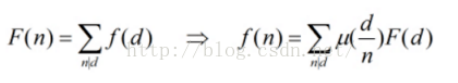
F(k)=(x/k)*(y/k)

 很明显  根据公式来看  F(d)是已知的，

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<cstring>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<algorithm>
#include<string>
#define ll long long
#define eps 1e-10
#define LL unsigned long long
using namespace std;
const int INF=0x3f3f3f3f;
const int N=1000000+100;
const int mod=998244353;
ll mu[N];
void getmu(){
    ll flag=0;
    for(int i=1;i<N;i++){
        if(i==1)flag=1;
        else{
            flag=0;
        }
        ll t=flag-mu[i];
        mu[i]=t;
        for(int j=2*i;j<N;j=j+i){
            mu[j]=mu[j]+t;
        }
    }
}
int main(){
    int t;
    getmu();
    //for(int i=1;i<=10;i++)cout<<mu[i]<<" ";
    //cout<<endl;
    scanf("%d",&t);
    int a,b,c,d,k;
    int Case=1;
    while(t--){
        int flag=0;
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
        if(k==0){
            printf("Case %d: ",Case++);
            cout<<0<<endl;
            continue;
        }
        b=b/k;
        d=d/k;
        ll ans=0;
        int minn=min(b,d);
        for(int i=1;i<=minn;i++){
            ans=ans+mu[i]*(b/i)*(d/i);
        }
        ll ans1=0;
        for(int i=1;i<=minn;i++){
            ans1=ans1+(mu[i]*(minn/i)*(minn/i));
        }
        printf("Case %d: ",Case++);
        cout<<ans-ans1/2<<endl;
    }

}