线段树和树状数组

线段树

引入1：有n个数（n<=50000）个数，m(m<=50000)次询问。每次询问区间L到R的数的和。要求输出每一次询问的结果......
分析：
1.用前缀和问题进行求解：再开一个数组（暂且记为b[n],设n个数所组成的数组为a[n]），b[i]用来记录从a[1]到a[i]的所有数字的和（即 b[1]=a[1],b[2]=b[1]+a[2],...,b[i]=b[i-1]+a[i]）。这样对于m次询问，只需要对数组b进行相应的操作就可以了。
eg:求数组a中区间[L,R]的所有数字的和sum，即sum=a[L]+a[L+1]+...+a[R-1]+a[R]。由于我们之前已经对数组a求了前缀和，并得到前缀和数组b[n]。因此对b[n]进行操作就可以了,即sum=b[R]-b[L-1]。
2.用线段树进行求解：这里先告诉大家可以用线段树来进行求解，具体如何求解我们可以等对线段树进行一定的讲解后再来进行求解。
引入2：RMQ(Range Minimum/Maximum Query)问题
有n(n<=50000)个数，m(m<=50000)次询问，要求每次输出区间[L,R]的数的最大值。
分析：
1.用ST表进行求解：一种利用dp思想求解区间最值的倍增算法。
定义：f(i,j)表示[i,i+\(2^j\)−1]这段长度为2^j的区间中的最大值。
预处理：f(i,0)=a[i]。即[i,i]区间的最大值就是a[i]。
状态转移：将[i,j]平均分成两段，一段为[i,i+2^{(j−1)−1]，另一段为[i+2}(j−1),i+2^{j−1]。两段的长度均为2}(j−1)。f(i,j)的最大值即这两段的最大值中的最大值。得到f(i,j)=max{f(i,j−1),f(i+2^(j−1),j−1)}。
查询：若需要查询的区间为[i,j]，则需要找到两个覆盖这个闭区间的最小幂区间。
这两个区间可以重复，因为两个区间是否相交对区间最值没有影响。（如下图）

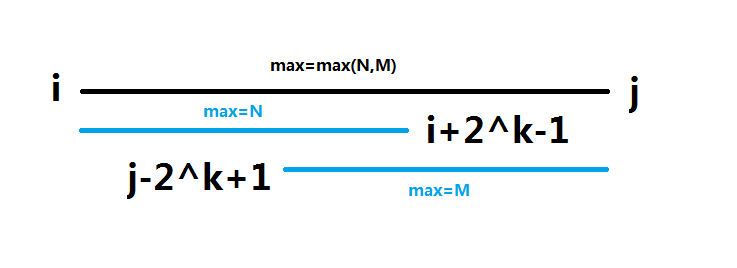
当然求区间和就肯定不行了。这也就是RMQ的限制性。
因为区间的长度为j−i+1，所以可以取k=\(\log_2 (j-i+1)\)。
则所求即为max{f(i,k),f(j−2k+1,k)}。
参考代码如下：

#include<iostream>//这段代码以询问最大值为例
#include<algorithm>
#include<cmath>
using namespace std;
int a[50005];
int f[50005][16];
int main()
{
    ios::sync_with_stdio(false);
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    cin>>a[i];
    for(int i=1;i<=n;i++)
    f[i][0]=a[i];//可以参照上文的预处理部分
    /*
    注意外部循环从j开始，
    因为初始状态为f[i][0],
    以i为外层会有一些状态遍历不到。
    */ 
    for(int j=1;j<=16;j++)//2^16>50000足够了
       for(int i=1;i<=n;i++)//可以参照上文的状态转移部分
          if(i+(1<<j)-1<=n)//判断区间最右端的值是否超过n
          {
              f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
          }
    int l,r;
    while(m--)//处理m次询问
    {
        cin>>l>>r;
        int k=(int)(log((double)(r-l+1))/(log(2.0)));
        cout<<max(f[l][k],f[r-(1<<k)+1][k])<<endl;
    }
    return 0;
}

参考例题：
【模板】ST表
质量检测
2.用线段树进行求解：这里先告诉大家可以用线段树来进行求解，具体如何求解我们可以等对线段树进行一定的讲解后再来进行求解。
概念：
线段树是用一种树状结构来存储一个连续区间的信息的数据结构。它主要用于处理一段连续区间的插入，查找，统计，查询等操作。
复杂度：设区间长度是n,所有操作的复杂度是logn级别。

• 线段树也是一种树形结构，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶节点。线段树是建立在线段的基础上，每个节点都代表了一条线段[a，b]，长度为 1 的线段称为元线段。非元线段都有两个子节点，左节点代表的线段为[a，（a+b）/2]，右节点代表的线段为[（（a+b）/2）+1，b]。
• 线段[1,7]的线段树和[2,5]的分解
  
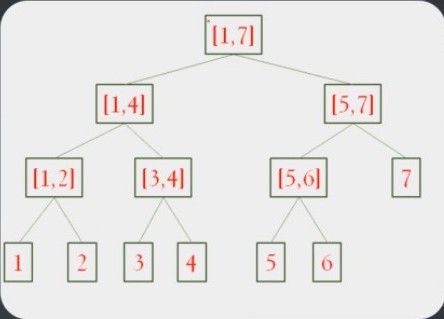
  线段树的几点性质：
• 线段树是平衡的二叉树，最大深度logn(n为线段树所表示区间的长度)
• 树中的每一个节点代表对应一个区间（叶子节点是一个点……）
• 每个节点（所代表的区间）完全包含它的所有孙节点
• 对于任意两个节点（所代表的区间）：要么完全包含，要么互不相交
• 在进行区间操作和统计时把区间等价转化成若干个子区间（logn个）的相同操作
• 任意的线段[a,b]在线段树的查询或查找过程中把这个线段最多分成log(b-a)份（显然每一层最多两个区间）
• So，线段树除建树外的操作都是log(n)级别的复杂度。
  使用线段树可以快速查找某个节点在若干条区间中出现的次数、某个区间的最大或最小值、某个区间的和等问题。这时就需要了解线段树的 3 个基本操作：建树、更新和查询。

例1：
给你一个长度为n的序列，有如下操作，将第i个数加或减x，求区间Li到Ri的和。
解析：
1：建树
-建树时，可以使用结构体的方法，将节点的左右端点、记录的信息（最大值、最小值、区间和等）存储进去；也可使用一个数组保存，使用数组时，省略了左右端点，因为在递归过程中，左右端点可以通过值传递的方式得到。建树就是一个遍历二叉树的过程，从根节点出发，依次遍历左子树，到元线段返回，再遍历右子树，直到遍历结束。
建树过程代码如下：

void buildTree(int p, int l,int r)//p:数组下标；l:区间左端点；r:区间右端点
{
    if(l==r)  
    {
        tree[p]=arr[l];
        return;
    }
    int mid=(l+r)/2;
    buildTree(p*2,l,mid);//建立左子树
    buildTree(p*2+1,mid+1,r);//建立右子树
    tree[p]=tree[p*2]+tree[p*2+1];
}

-更新操作和查询操作类似，时间复杂度都为O(logn)。当执行更新操作时，要遍历到叶子节点，再层层递归更新,而查询操作只需要查询到包括的区间为止。
更新操作如下：

void change(int p,int l, int r,int x, int num)//给下标为x的位置加上num
{
    if(l==r)
    {
        tree[p]+=num;
        return;
    }
    int mid=(l+r)/2;
    if(x<=mid)
    {
        change(p*2,l,mid,x,num);
    }
    else
    {
        change(p*2+1,mid+1,r,x,num);
    }
    tree[p]=tree[p*2]+tree[p*2+1];
}

查询操作如下：

int query(int p,int l,int r, int x, int y)
{
    if(x<=l&&r<=y)
    return tree[p];
    int mid=(l+r)/2;
    if(y<=mid)
    return query(p*2,l,mid,x,y);
    if(x>mid)
    return query(p*2+1,mid+1,r,x,y);
    return (query(p*2,l,mid,x,y)+query(p*2+1,mid+1,r,x,y));
}

完整代码如下：

#include<iostream>
using namespace std;
int arr[10005],tree[10005];
void buildTree(int p, int l,int r)//p:数组下标；l:区间左端点；r:区间右端点
{
    if(l==r)  
    {
        tree[p]=arr[l];
        return;
    }
    int mid=(l+r)/2;
    buildTree(p*2,l,mid);//建立左子树
    buildTree(p*2+1,mid+1,r);//建立右子树
    tree[p]=tree[p*2]+tree[p*2+1];
}
void change(int p,int l, int r,int x, int num)//给下标为x的位置加上num
{
    if(l==r)
    {
        tree[p]+=num;
        return;
    }
    int mid=(l+r)/2;
    if(x<=mid)
    {
        change(p*2,l,mid,x,num);
    }
    else
    {
        change(p*2+1,mid+1,r,x,num);
    }
    tree[p]=tree[p*2]+tree[p*2+1];
}
int query(int p,int l,int r, int x, int y)
{
    if(x<=l&&r<=y)
    return tree[p];
    int mid=(l+r)/2;
    if(y<=mid)
    return query(p*2,l,mid,x,y);
    if(x>mid)
    return query(p*2+1,mid+1,r,x,y);
    return (query(p*2,l,mid,x,y)+query(p*2+1,mid+1,r,x,y));
}
int main()
{
    ios::sync_with_stdio(false);
    int n,m,k;//n个元素，m次修改,k次询问
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)
    cin>>arr[i];
    buildTree(1,1,n);
   while(m--)
    {
        int x,num;
        cin>>x>>num;
        change(1,1,n,x,num);
    }
    while(k--)
    {
        int x,y;
        cin>>x>>y;
        cout<<query(1,1,n,x,y)<<endl;
    }
    return 0;
}

线段树和树状数组的题单：https://ac.nowcoder.com/acm/problem/collection/621
参考资料：
1.https://www.cnblogs.com/YSFAC/p/7189571.html
2.https://www.cnblogs.com/TheRoadToTheGold/p/6254255.html