深度搜索专题

蓝桥杯之带分数

最近在蓝桥杯中遇到很多的题，类似于将1-9的数字 全部排列出来，满足一个条件，比如这个带分数的题。就需要用1-9所有的数。

这里就运用深度搜索来做。在一个数组中，将全部的1-9这九个数字全部排列出来。

代码如下：

public class Main {
	static int[] a = new int[10];//1-9这9个数字是否访问过的状态数组
	static int[] b = new int[10];//需要排列的数组

	public static void main(String[] args) {
		dfs(1);
	}

	static void dfs(int i) {
		if (i > 9) {
			for (int k = 1; k <= 9; k++) {
				System.out.print(b[k]);
			}
			System.out.println();
			return;//满足条件后输出
		} else {
			for (int j = 1; j <= 9; j++) {
				if (a[j] == 0) {//判断是否某某数字已经出现过
					a[j] = 1;//将该数字的状态置为1
					b[i] = j;//将该位置i置为数字j
					dfs(i + 1);//跳向下一个数字
					b[i] = 0;// 回溯
					a[j] = 0;// 回溯
				}
			}
		}
		return;
	}
}

　　

一维深搜：

public class Main {
	static int n1;
	static int[] arr;
	static int n2;
	static int Count = 0;
	static int[] brr;
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		n1 = scan.nextInt();
		arr = new int[n1];
		n2 = scan.nextInt();
		brr=new int[n2+1];
		for (int i = 0; i < n1; i++) {
			arr[i] = scan.nextInt();
		}
		dfs(0,1);
		System.out.println(Count);
	}
	
	//
	static void dfs(int i,int count) {
		//一维遍历深搜
		//退出递归条件
		if(i<=n1){//之所以要==n1，会将arr元素组中最后一个元素遍历装进了brr中。不然会少掉这种。
			if(count==n2+1){//如果当前brr中元素为3个。这里的加一的原因是数组是从1开始的，0没有用
				//这个地方是为了呼应后面判断大小arr[j]>brr[count-1]。
				//装第一个元素的时候，可以直接装进去，因为brr[0]为0可以直接装进进去
					Count++;//并且里面肯定装的是 递增元素，因为是判断必须比brr结果数组前一个大的数，才能够放进数组
				return;
			}
		}else{
			return;
		}
		for(int j=i;j<n1;j++){//从当前进来这个位置开始遍历，因为上一次传入的是j+1，题意是按从前到后的顺序找升序。
			if(arr[j]>brr[count-1]){//判断当前遍历的数与brr结果数组中的最后一个值进行比较大小。如果大，就存入brr。
				brr[count]=arr[j];
				dfs(j+1,count+1);//因为已经遍历到了当前的j位置所以下一次从j+1开始遍历
				brr[count]=0;//回溯
			} 
		}
		return;
	}

　　

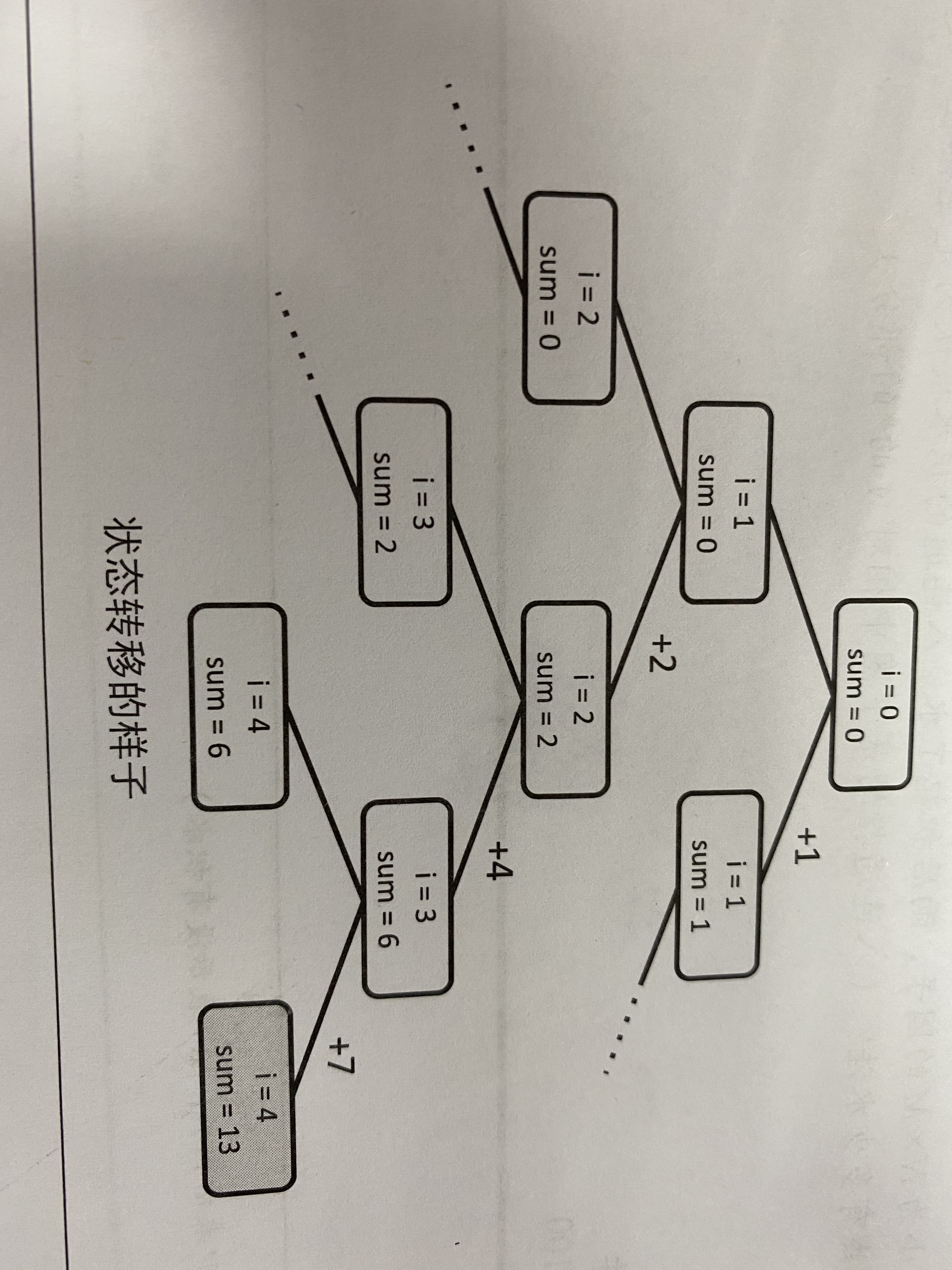
问题：从给定整数a1、a2 ... an中，判断是否可以从中选出若干数，使它们的和恰好为k。

输入：

n=4;

a[{1,2,4,7};

k=13;

输出：yes

代码：

public class Main {
	static int MAX_N;
	static int[] a;
	static int n,k;
	public static void main(String[] args) {
		

a=new int[]{1,2,4,7};
		k=14;
		n=4;
		if(dfs(0,0)==true)
			System.out.println("yes");
		else
			System.out.println("no");
	}
	
	static boolean dfs(int i,int sum){//i代表遍历的指针。
		if(i==n)//当遍历完了所有的值。
			return sum==k;
		if(dfs(i+1,sum))//遍历下一个，不加当前的值。
			return true;
		if(dfs(i+1,sum+a[i]))//遍历下一个，加上当前的值。
			return true;
		return false;//未遍历到，return false;一直返回false;
	}
}