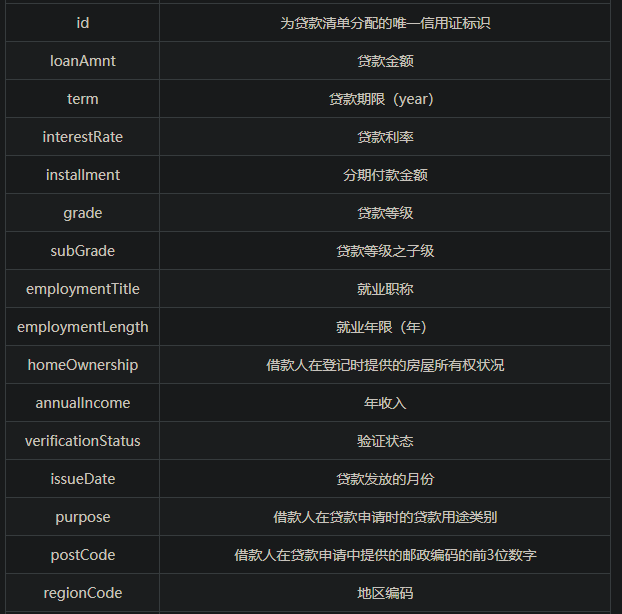
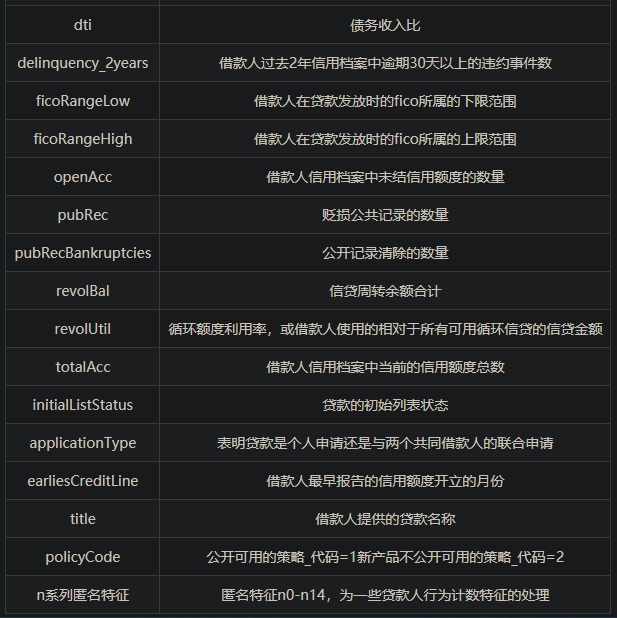
赛题数据
赛题以预测用户贷款是否违约为任务,数据集报名后可见并可下载,该数据来自某信贷平台的贷款记录,总数据量超过120w,包含47列变量信息,其中15列为匿名变量。为了保证比赛的公平性,将会从中抽取80万条作为训练集,20万条作为测试集A,20万条作为测试集B,同时会对employmentTitle、purpose、postCode和title等信息进行脱敏。
字段如下
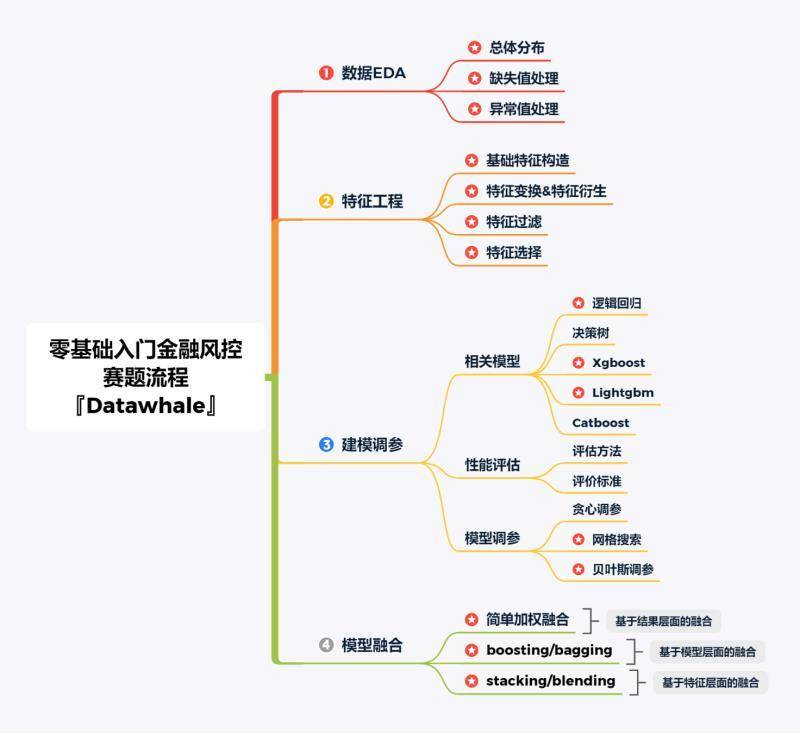
解题思路
评测标准
提交结果为每个测试样本是1的概率,也就是y为1的概率。评价方法为AUC评估模型效果(越大越好)。
关于评测指标
1、混淆矩阵(Confuse Matrix)
- 若一个实例是正类,并且被预测为正类,即为真正类TP(True Positive )
- 若一个实例是正类,但是被预测为负类,即为假负类FN(False Negative )
- 若一个实例是负类,但是被预测为正类,即为假正类FP(False Positive )
- 若一个实例是负类,并且被预测为负类,即为真负类TN(True Negative )
代码示例:
## 混淆矩阵
import numpy as np
from sklearn.metrics import confusion_matrix
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('混淆矩阵:
',confusion_matrix(y_true, y_pred))
2、准确率(Accuracy)
准确率是常用的一个评价指标,但是不适合样本不均衡的情况。 $$Accuracy = frac{TP + TN}{TP + TN + FP + FN}$$
## accuracy
from sklearn.metrics import accuracy_score
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('ACC:',accuracy_score(y_true, y_pred))
3、精确率(Precision)
又称查准率,正确预测为正样本(TP)占预测为正样本(TP+FP)的百分比。 $$Precision = frac{TP}{TP + FP}$$
## Precision
from sklearn import metrics
y_pred = [0, 1, 0, 1]
y_true = [0, 1, 1, 0]
print('Precision',metrics.precision_score(y_true, y_pred))
4、召回率(Recall)
又称为查全率,正确预测为正样本(TP)占正样本(TP+FN)的百分比。 $$Recall = frac{TP}{TP + FN}$$
## Recall
print('Recall',metrics.recall_score(y_true, y_pred))
5、F1 Score
精确率和召回率是相互影响的,精确率升高则召回率下降,召回率升高则精确率下降,如果需要兼顾二者,就需要精确率、召回率的结合F1 Score。 $$F1-Score = frac{2}{frac{1}{Precision} + frac{1}{Recall}}$$
## F1-score
print('F1-score:',metrics.f1_score(y_true, y_pred))
6、P-R曲线(Precision-Recall Curve)
P-R曲线是描述精确率和召回率变化的曲线
## P-R曲线
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
precision, recall, thresholds = precision_recall_curve(y_true, y_pred)
plt.plot(precision, recall)

7、ROC(Receiver Operating Characteristic)
- ROC空间将假正例率(FPR)定义为 X 轴,真正例率(TPR)定义为 Y 轴。
TPR:在所有实际为正例的样本中,被正确地判断为正例之比率。 $$TPR = frac{TP}{TP + FN}$$ FPR:在所有实际为负例的样本中,被错误地判断为正例之比率。 $$FPR = frac{FP}{FP + TN}$$
from sklearn.metrics import roc_curve
y_pred = [0, 1, 1, 0, 1, 1, 0, 1, 1, 1]
y_true = [0, 1, 1, 0, 1, 0, 1, 1, 0, 1]
FPR,TPR,thresholds=roc_curve(y_true, y_pred)
plt.title('ROC')
plt.plot(FPR, TPR,'b')
plt.plot([0,1],[0,1],'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')

8、AUC(Area Under Curve)
被定义为 ROC曲线 下与坐标轴围成的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。AUC越接近1.0,检测方法真实性越高;等于0.5时,则真实性最低,无应用价值。
## AUC
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:',roc_auc_score(y_true, y_scores))
扩展知识:金融风控预测类常见的评估指标
1、KS(Kolmogorov-Smirnov)
2、ROC
3、AUC
下面介绍下KS:
KS统计量由两位苏联数学家A.N. Kolmogorov和N.V. Smirnov提出。
在风控中,KS常用于评估模型区分度。区分度越大,说明模型的风险排序能力(ranking ability)越强。 K-S曲线与ROC曲线类似,不同在于
- ROC曲线将真正例率和假正例率作为横纵轴
- K-S曲线将真正例率和假正例率都作为纵轴,横轴则由选定的阈值来充当。 公式如下: $$KS=max(TPR-FPR)$$ KS不同代表的不同情况,一般情况KS值越大,模型的区分能力越强,但是也不是越大模型效果就越好,如果KS过大,模型可能存在异常,所以当KS值过高可能需要检查模型是否过拟合。以下为KS值对应的模型情况,但此对应不是唯一的,只代表大致趋势。
| KS(%) | 好坏区分能力 |
|---|---|
| 20以下 | 不建议采用 |
| 20-40 | 较好 |
| 41-50 | 良好 |
| 51-60 | 很强 |
| 61-75 | 非常强 |
| 75以上 | 过于高,疑似存在问题 |