最短路径问题-Dijkstra算法

算法介绍

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

基本思想

     通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

     此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

     初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是"起点s到该顶点的路径"。然后，从U中找出路径最短的顶点，并将其加入到S中；接 着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 ... 重复该操作，直到遍历完所有顶点。

操作步骤

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

(2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。

(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

(4) 重复步骤(2)和(3)，直到遍历完所有顶点。

 时间复杂度：o(n^2).

求v0到v8的最短路径：

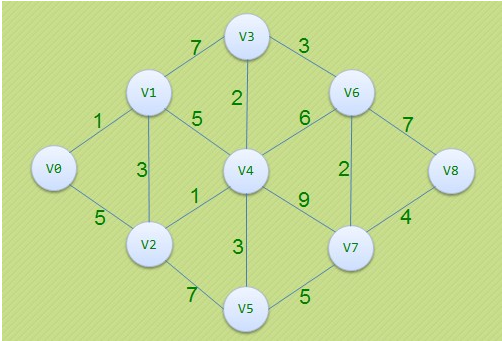
 代码如下：

#include <stdio.h>

#define MAXVEX 9
#define MAXEDGES 16
#define INFINITE 60000

//定义图的类型
typedef struct {
    int vexs[MAXVEX];//保存顶点名称
    int arc[MAXVEX][MAXVEX];//邻接矩阵
    int numVertexs,numEdges;
}MGraph;

typedef int Patharc[MAXVEX];    //存储最短路径的情况下，每个顶点的上一个顶点
typedef int ShortPathTable[MAXVEX];    //存储v0到各个顶点最短路径的长度

//构建图
void CreateMGraph(MGraph * G){
    int i,j;
    G->numEdges=16;
    G->numVertexs=9;
    //给每个顶点命名
    for(i=0; i<G->numVertexs; i++){
        G->vexs[i]=i;
    }

    for(i=0; i<G->numVertexs; i++){
        for(j=0; j<G->numVertexs; j++){
            if(i==j){
                G->arc[i][j]=0;
            }else{
                G->arc[i][j]=INFINITE;
            }
        }
    }

    G->arc[0][1]=1;
    G->arc[0][2]=5; 
    G->arc[1][2]=3; 
    G->arc[1][3]=7; 
    G->arc[1][4]=5; 

    G->arc[2][4]=1; 
    G->arc[2][5]=7; 
    G->arc[3][4]=2; 
    G->arc[3][6]=3; 
    G->arc[4][5]=3;

    G->arc[4][6]=6;
    G->arc[4][7]=9; 
    G->arc[5][7]=5; 
    G->arc[6][7]=2; 
    G->arc[6][8]=7;

    G->arc[7][8]=4;

    for(i=0;i<G->numVertexs; i++){
        for(j=0; j<i; j++){
            G->arc[i][j]=G->arc[j][i];
        }
    }
}

/*  Dijkstra算法，求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度D[v] */    
/*  P[v]的值为前驱顶点下标,D[v]表示v0到v的最短路径长度和 */  
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D){
    int i,j,k,w;
    int final[MAXVEX];//如果找到到某顶点的最短路径，就标记1，初始为-1

    for(i=0; i<G.numVertexs; i++){
        (*P)[i]=0;//初始P[]为0
        final[i]=-1;
        (*D)[i]=G.arc[0][i];//初始化顶点0到其他顶点的长度
    }

    final[0]=1;//到0的最短路径已经找到了，就是本身
    

    for(i=1; i<G.numVertexs; i++){//以下的1，2，3，步骤，每进行一次会确定一个不同的顶点，
        //使得v0到该顶点的距离最短，如此循环G.numVertexs-1次，可以找到v0到其余所有顶点的最短路径
        
        //1.找v0到各个顶点最短的路径
        int min=INFINITE;
        for(j=1; j<G.numVertexs; j++){
            if(final[j]!=1 && (*D)[j] < min){
                min=(*D)[j];
                k=j;
            }
        }

        //2.顶点k的最短路径已经找到，就是min(找到一个做一次标记)
        final[k]=1;
        
        //3. 如果经过v顶点的路径比现在这条路径的长度短的话，更新v0到该顶点的距离，否则不进行任何操作
        for(w=1; w<G.numVertexs; w++){
            if(final[w]!=1 && min+G.arc[k][w] < (*D)[w]){
                /*  说明找到了更短的路径，修改D[w]和P[w] */
                (*D)[w]=min+G.arc[k][w];
                (*P)[w]=k;
            }
        }

    }
}

int main(){

MGraph G;
int i,j,t,v0=0;
Patharc P;
ShortPathTable D;

CreateMGraph(&G);

ShortestPath_Dijkstra(G, v0, &P, &D);

    //打印
    for(j=1; j<G.numVertexs; j++){

        printf("v%d-->v%d的最短路径长度为%d
",v0,j,D[j]);
        
        t=j;
        printf("最短路径倒叙为v%d-->",t);
            while(P[t]!=0){
            printf("v%d-->",P[t]);
            t=P[t];
            }
        printf("v%d

",P[t]);
    }
return 0;
}

结果：