【洛谷】训练场_递推与递归二分场（不全）

P1192 台阶问题

分析：

与P1255数楼梯题意一样，只不过数据不一样，数楼梯一题是涉及高精度与字符串处理。

如果数据不大，且每次最多只能迈2级阶梯的话，本题则是斐波那契数列的裸题。

1阶：1

2阶：2

3阶：1阶+2阶（1阶时迈2步，2阶时迈1步）

以次类推；

这题写多了几个K后，我发现了一个新的规律：

当K=4时；

0阶：0

1阶：1（0阶+1）

2阶：2（0阶+1阶+1）

3阶：4（0阶+1阶+2阶+1）

4阶：8（0阶+1阶+2阶+3阶+1）

5阶：16（1阶+2阶+3阶+4阶）因为0阶加不加都无所谓可以去掉

6阶：30（2阶+3阶+4阶+5阶）

以此类推；

思路是一样的，求第4阶的方案数，等于在第1阶上迈3步+在第2阶上迈2步+在第三阶迈1步+直接在底层（0阶）迈4步他们的方案数的总和。

剩下的就是类似斐波那契数列的处理了。

题目要求输出的 ans 要 mod 100003 ，因此我们只要知道 (a + b) % c = [(a%c) + (b%c)] % c 即可

（这里就不证明了，网上有很多大牛的解释）

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

const int MOD = 100003;
int N, K;
long long num[102];
int ans;

int main()
{
    while(cin >> N >> K){
        // 类斐波那契数列前的处理
        ans = 0;
        memset(num, 0, sizeof(num));
        num[0] = 0; num[1] = 1; num[2] = 2;
        for(int i = 3; i <= K; i++){
            for(int j = 0; j < i; j++){
                num[i] += num[j] % MOD;
            }
            num[i] %= MOD;
            num[i] = (num[i]%MOD + 1%MOD) % MOD;
        }
        //开始走楼梯
        for(int i = K+1; i <= N; i++){
            ans = 0;
            for(int j = 1; j <= K; j++){
                ans += num[j]%MOD;
                ans %= MOD;
                if(j==K) num[j] = ans;
                else num[j] = num[j+1];
            }
        }
        // 注意要比较 N 与 K 的大小比较
        if(N >= K) cout << num[K] << endl;
        else cout << num[N] << endl;

    }
    return 0;
}

下一题：

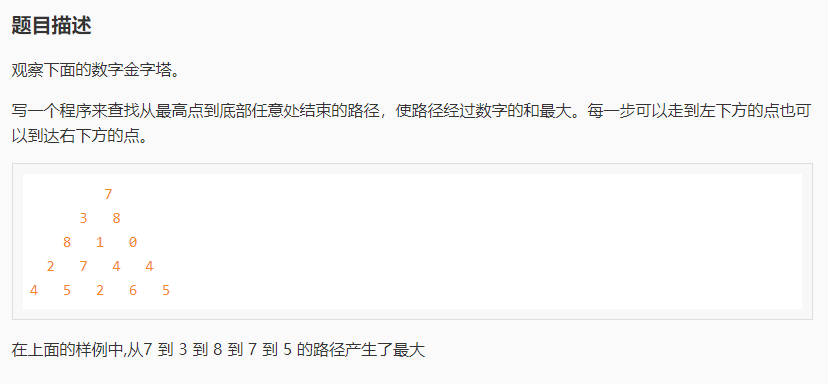
 P1216 [IOI1994][USACO1.5]数字三角形 Number Triangles

分析：

R最大是1000，那二维数组可以开出来，想到之前刚学会的回溯，这样就可以遍历所有情况再输出最大值就OK。

没错，以上是TLE的思路。

#include<iostream>
#include<cstdio>
using namespace std;

int R;
int tri[1001][1001];
int ans, tot;

void down(int a, int b){
    if(a == R) {
        tot += tri[a][b];
        if(tot > ans) ans = tot;
        return ;
    }
    else {
        tot += tri[a][b];
        down(a+1, b);
        tot -= tri[a+1][b];
        down(a+1, b+1);
        tot -= tri[a+1][b+1];
    }
    return ;
}
int main()
{
    while(cin >> R){
        tot = ans = 0;
       for(int i = 1; i <= R; i++){
        for(int j = 1; j <= i; j++){
            cin >> tri[i][j];
        }
       }

       down(1, 1);

       cout << ans << endl;
    }
    return 0;
}

然后瞄了一眼题解——还真是以前做过的题呀！

DP算法，从下往上算。

比如例子倒数第1行与倒数第二行

  2  7  4  4

4  5  2  6  5

从倒数第二行开始，只需比较4， 5谁大，谁大和2相加并保存。

以此从下往上堆砌，最后得到的第一层即是最大值。

#include<iostream>
#include<algorithm>
using namespace std;

int R;
int ans[1001][1001];

int main()
{
    while(cin >> R){
        for(int i = 1; i <= R; i++)
        for(int j = 1; j <= i; j++)
            cin >> ans[i][j];

        for(int i = R-1; i >= 1; i--)
        for(int j = 1; j <= i; j++)
            ans[i][j] += max(ans[i+1][j], ans[i+1][j+1]);

       cout << ans[1][1] << endl;
    }
    return 0;
}