Educational Codeforces Round 41 (Rated for Div. 2) G. Partitions

G. Partitions

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a set of n elements indexed from 1 to n. The weight of i-th element is wi. The weight of some subset of a given set is denoted as 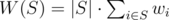. The weight of some partition R of a given set into k subsets is  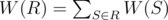(recall that a partition of a given set is a set of its subsets such that every element of the given set belongs to exactly one subset in partition).

Calculate the sum of weights of all partitions of a given set into exactly k non-empty subsets, and print it modulo 109 + 7. Two partitions are considered different iff there exist two elements x and y such that they belong to the same set in one of the partitions, and to different sets in another partition.

Input

The first line contains two integers n and k (1 ≤ k ≤ n ≤ 2·105) — the number of elements and the number of subsets in each partition, respectively.

The second line contains n integers wi (1 ≤ wi ≤ 109)— weights of elements of the set.

Output

Print one integer — the sum of weights of all partitions of a given set into k non-empty subsets, taken modulo 109 + 7.

Examples

input

Copy

4 2
2 3 2 3

output

Copy

160

input

Copy

5 2
1 2 3 4 5

output

Copy

645

Note

Possible partitions in the first sample:

1. {{1, 2, 3}, {4}}, W(R) = 3·(w1 + w2 + w3) + 1·w4 = 24;
2. {{1, 2, 4}, {3}}, W(R) = 26;
3. {{1, 3, 4}, {2}}, W(R) = 24;
4. {{1, 2}, {3, 4}}, W(R) = 2·(w1 + w2) + 2·(w3 + w4) = 20;
5. {{1, 3}, {2, 4}}, W(R) = 20;
6. {{1, 4}, {2, 3}}, W(R) = 20;
7. {{1}, {2, 3, 4}}, W(R) = 26;

Possible partitions in the second sample:

1. {{1, 2, 3, 4}, {5}}, W(R) = 45;
2. {{1, 2, 3, 5}, {4}}, W(R) = 48;
3. {{1, 2, 4, 5}, {3}}, W(R) = 51;
4. {{1, 3, 4, 5}, {2}}, W(R) = 54;
5. {{2, 3, 4, 5}, {1}}, W(R) = 57;
6. {{1, 2, 3}, {4, 5}}, W(R) = 36;
7. {{1, 2, 4}, {3, 5}}, W(R) = 37;
8. {{1, 2, 5}, {3, 4}}, W(R) = 38;
9. {{1, 3, 4}, {2, 5}}, W(R) = 38;
10. {{1, 3, 5}, {2, 4}}, W(R) = 39;
11. {{1, 4, 5}, {2, 3}}, W(R) = 40;
12. {{2, 3, 4}, {1, 5}}, W(R) = 39;
13. {{2, 3, 5}, {1, 4}}, W(R) = 40;
14. {{2, 4, 5}, {1, 3}}, W(R) = 41;
15. {{3, 4, 5}, {1, 2}}, W(R) = 42.

思路一：考虑每个点对整体的贡献。也就是SUM (size * S(n - size, k - 1) )* wi， S(n, k)为第二类斯特林数。但这样需求出所有的S(i, k - 1)，暂时不会nlogn求法。复杂度O(n*k)。

思路二：定义g(n, k, i, j)表示n个数分成k个非空集合且i与j在一个集合中的方案数。单独对一个点ai考虑，对于每一个合法的划分，它的贡献要有size次，size为ai所在集合的大小。那么对于SUM(g(n, k, i, j)),其中j从1遍历到n，在这些所有的方案中，我们之前考虑的特定的那个划分也正好出现了size次，两个数刚好等价了。所以答案就是g(n, k, i, i) + SUM(g(n, k, i, j) (j != i)) = S(n, k) + (n - 1) * S(n - 1, k)。对于单点斯特林数，可以通过容斥加快速幂nlogn求出。

S(n, k) = SUM((-1) ^ i * C(k, i) * (k - i) ^ n) / k!。复杂度nlogn。

#include <iostream>
#include <fstream>
#include <sstream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <list>
#include <iomanip>
#include <cctype>
#include <cassert>
#include <bitset>
#include <ctime>

using namespace std;

#define pau system("pause")
#define ll long long
#define pii pair<int, int>
#define pb push_back
#define mp make_pair
#define clr(a, x) memset(a, x, sizeof(a))

const double pi = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const double EPS = 1e-9;

/*
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

using namespace __gnu_pbds;
tree<pli, null_type, greater<pli>, rb_tree_tag, tree_order_statistics_node_update> T;
*/

int n, k;
ll W, N[400015];
ll mpow(ll x, ll y) {
    if (!y) return 1;
    ll res = mpow(x, y >> 1);
    if (y & 1) return res * res % MOD * x % MOD;
    return res * res % MOD;
}
void pre() {
    N[0] = 1;
    for (int i = 1; i <= 400000; ++i) {
        N[i] = N[i - 1] * i % MOD;
    }
}
ll inv(ll x) {
    return mpow(x, MOD - 2);
}
ll C(int n, int k) {
    return N[n] * inv(N[n - k]) % MOD * inv(N[k]) % MOD;
}
ll stirling(ll x, ll y) {
    ll res = 0;
    for (int i = 0; i < y; ++i) {
        if (i & 1) res -= C(y, i) * mpow(y - i, x) % MOD;
        else res += C(y, i) * mpow(y - i, x) % MOD;
    }
    res = (res % MOD + MOD) % MOD;
    return res * inv(N[y]) % MOD;
}
int main() {
    pre();
    scanf("%d%d", &n, &k);
    for (int i = 1, w; i <= n; ++i) {
        scanf("%d", &w);
        W += w;
    }
    printf("%lld
", W % MOD * (stirling(n, k) + (n - 1) * stirling(n - 1, k) % MOD) % MOD);
    return 0;
}