UVA297 四分树 Quadtrees
题目描述(。。)
输入格式

输出格式

题意翻译
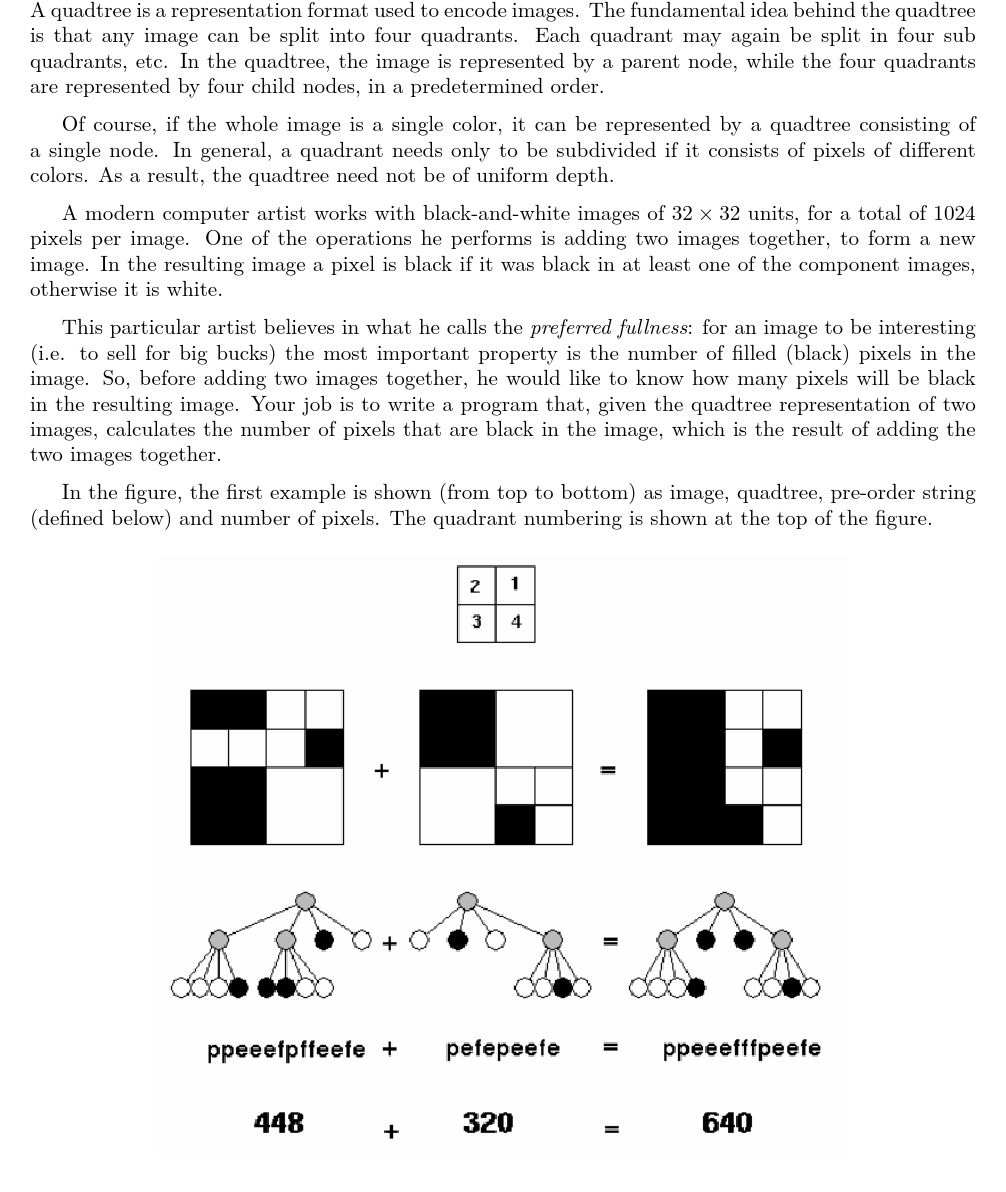
如图所示,可以用四分图来表示一个黑白图像,方法是用根节点表示整幅图像,然后把行列个分成两等份,按图中的方式编号,从左到右对应4个子节点。如果某子节点对应的区域全黑或全白,则直接用一个黑节点或白节点表示;如既有黑又有白,则用一个灰节点表示,并且为这个区域递归建树。 给出两棵四分树的先序遍历,求二者合并(黑色部分合并)黑像素的个数(每幅图都是32X32的)。p表示灰节点,f表示黑节点,e表示白节点。 具体内容看原文和紫书。
感谢 @happyZYM 提供的翻译。
输入输出样例
输入 #1
3
ppeeefpffeefe
pefepeefe
peeef
peefe
peeef
peepefefe
输出 #1
There are 640 black pixels.
There are 512 black pixels.
There are 384 black pixels.
思路
-
注意顺序(依次为右上,左上,左下,右下),这在写递归代码时非常重要。
-
合并=在原来的基础上覆盖
-
不断地缩小规模
-
遇到颜色,直接对范围内地方块全部进行涂色。
-
当然,如果是空白,就没有必要再对范围内的方块的颜色进行清零。
-
递归的材料:
- 左上角的点
- 左上角点的x
- 左上角点的y
- 方块的长度
- 字符串
- 读取的位置(引用比较指针好用)
- 左上角的点
-
细节:
-
单方向的范围:初始点 到 初始点+长度-1
-
如果原本就是黑色了就没有必要对这个格子进行统计了
-
是对范围内的每一个格子进行检测
-
输出的处理
-
#include<iostream>
#include<stdio.h>
#include<string.h>
using namespace std;
int color[35][35];
int cnt;
void draw(string &s,int &order,int row,int col,int len)
{
order++;
if(s[order]=='p')
{
draw(s,order,row,col+len/2,len/2);
draw(s,order,row,col,len/2);
draw(s,order,row+len/2,col,len/2);
draw(s,order,row+len/2,col+len/2,len/2);
}
else if(s[order]=='f')
{
for(int i=row;i<row+len;i++)
{
for(int j=col;j<col+len;j++)
{
if(color[i][j]==0)
{
color[i][j]=1;
cnt++;
}
}
}
}
}
int main()
{
int n;
cin>>n;
while(n--)
{
string s;
memset(color,0,sizeof(color));
cnt=0;
for(int i=0;i<2;i++)
{
cin>>s;
int order=-1;
int len=32;
draw(s,order,0,0,len);
}
cout<<"There are "<<cnt<<" black pixels."<<endl;
}
return 0;
}
四分树为什么给出先序遍历后就是唯一的
四分树相对于二叉树,它的儿子的明确的不是二义的(二叉树中先序遍历的下一个字母有可能是它的儿子,也有可能是它的兄弟)